Algebra
Algebra
Your child may think that algebra sounds scary but with a bit of practice and working through some examples they’ll become more confident with the type of questions that they might be asked.
Algebra uses letters as a place holder when the value is unknown. Questions in this topic will often be about finding unknown values. We will be introducing a concept called BIDMAS which tells your child what order to work out operations such as division, multiplication, addition and subtraction.
What is Algebra?
The letter x is often used to represent a value that is unknown in an equation.
Example: x + 1 = 9
This means that 1 added to another number that is unknown equals 9. By working in reverse, subtracting 1 from both sides of the equation, we can find x.
x + 1 \textcolor{red}{- 1} = 9 \textcolor{red}{- 1}
x = 8
Multiplication and Division
When multiplying a number by an unknown, a multiplication sign isn’t often used. The letter being used to represent the unknown number can just be written next to the number.
4x = 4 \times x or a \times b = ab
Division also doesn’t need to be denoted by the usual symbol, \div. The values are more often written as fractions with the number you are dividing into as the numerator and the number you are dividing by as the denominator.
3 \times x \div 10 = \dfrac{3x}{10}
As with regular numbers, letters that are being used as placeholders for numbers can be squared. This means that the unknown value has been multiplied by itself.
y \times y = y^{2}
So, if y = 4, we could work out that:
y^{2} = 4^{2} = 4 \times 4 = 16
Brackets in Expressions
Brackets are an important method to keep algebra simplified and concise. It is important that your child is comfortable and familiar with what different expressions involving brackets mean.
Example: 5(x + y)
Breaking this expression down we can see that this means that there are 5 lots of the entire bracket (x+y).
(x + y) + (x + y) + (x + y) + (x + y) + (x + y) = 5(x + y)
It is important to keep everything that is in the brackets together as it is the entire bracket that is being multiplied by 5 not just one of the terms.
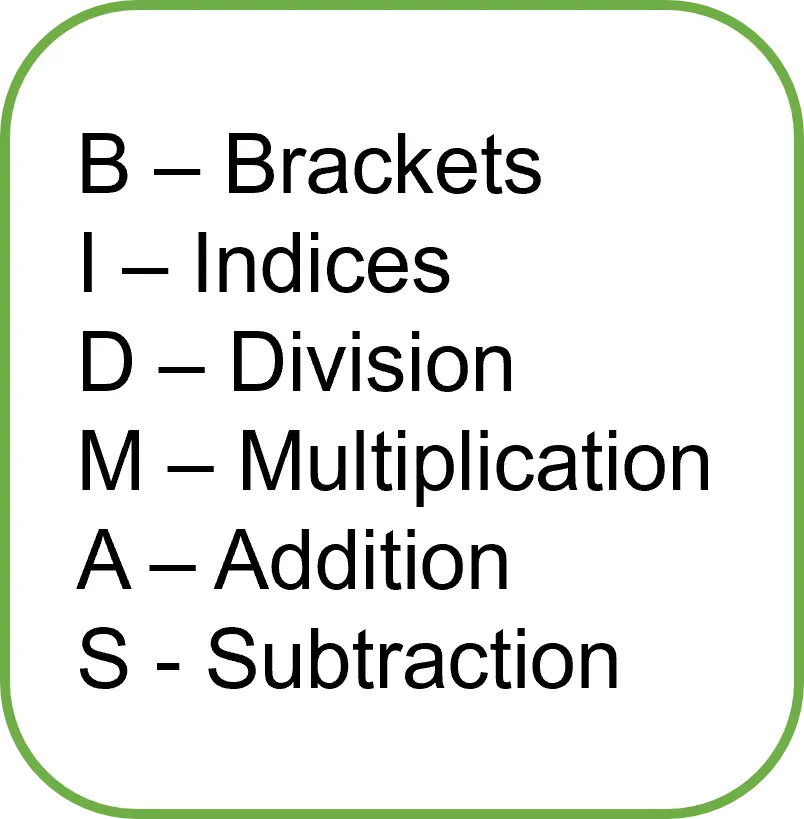
BIDMAS
BIDMAS, or BODMAS as it is sometimes referred to, is a way for your child to remember the order in which to perform operations when there are a few to do in the same expression.
B – Brackets
If there are any brackets in the expression, your child should tackle these first.
I or O – Indices or Order
This refers to any square numbers or cube numbers that may be in the calculation.
D – Division
M – Multiplication
Any \bold{\textcolor{darkturquoise}{\div}} or \bold{\textcolor{darkturquoise}{\times}} symbols need to be dealt with next.
A – Addition
S – Subtraction
Once each of the above has been dealt, your child should be left with \bold{\textcolor{darkturquoise}{+}} and \bold{\textcolor{darkturquoise}{-}} symbols which can then be dealt with to give the final answer.
Example 1: BIDMAS

Your child may come across BIDMAS in the context of algebraic expressions.
Example: Work out (14+x) \div 3^{2} + 10 when x =4
First, substitute in the value for x.
(14 + 4) \div 3^{2} + 10
There is a reminder of BIDMAS to the right so, let’s go through one by one.
Are there any brackets? Yes!
(14+4) = 18 so let’s put that back into the expression.
18 \div 3^{2} + 10
Are there any indices? Remind your child that this just means, are there any values being squared or cubed?
Yes, there are, we have 3^{2}.
3^{2} = 3 \times 3 = 9
So, we are left with 18 \div 9 +10
Is there any division in the remaining expression? Yes!
18 \div 9 = 2
Finally we are left with 2 + 10 =12
So, our final answer is 12
Example 2: Solving Equations
When solving an equation to find the unknown value, your child needs to do the opposite of the operations on the same side of the equals sign as the unknown value.
Example: Solve 6x - 5 = 13
The end goal for a question like this is to get the x on its own.
First, the opposite of \textcolor{red}{-5} is \textcolor{red}{+5}.
6x - 5 \textcolor{red}{+5} = 13 \textcolor{red}{+5}
6x = 18
Remind your child that 6x = 6 \times x and so the opposite of \textcolor{red}{\times 6} is \textcolor{red}{\div 6}.
6x \textcolor{red}{\div 6} = 18 \textcolor{red}{\div 6}
x=3
The x is now on one side of the equals sign on its own so we have solved the equation.
Algebra Example Questions
Question 1: Solve the following equations.
a) \dfrac{x}{8} + 3 = 5
b) 3(2+x) = 21
[2 marks]
a) The opposite of \textcolor{red}{+3} is \textcolor{red}{-3}
\dfrac{x}{8} + 3 \textcolor{red}{-3} = 5 \textcolor{red}{-3}
\dfrac{x}{8} = 2
The line of a fraction just means to divide. So, the opposite of \textcolor{red}{\div 8} is \textcolor{red}{\times 8}
\dfrac{x}{8} \textcolor{red}{\times 8} = 2 \textcolor{red}{\times 8}
x = 16
b) This equation is the same as:
3 \times (2 + x) = 21
We want to keep the bracket together for now.
The opposite of \textcolor{red}{\times 3} is \textcolor{red}{\div 3}.
3(2 + x) \textcolor{red}{\div 3} = 21 \textcolor{red}{\div 3}
As only the brackets are left on one side of the equation they are no longer needed!
2+x = 7
The opposite of \textcolor{red}{+2} is \textcolor{red}{-2}.
2 + x \textcolor{red}{-2} = 7 \textcolor{red}{-2}
x = 5
Question 2: Which of the following is the correct expression for the sequence below?
7,\,\,11,\,\,15,\,\,19
[1 mark]
A: 7n
B: 4n +3
C: 4n - 3
D: 7n + 3
Try out each of the options to see which one follows the sequence correctly.
Option A:
First term, \textcolor{blue}{n=1}: 7 \times 1 = 7 correct for the first term.
Second term, \textcolor{blue}{n=2}: 7 \times 2 = 14 which is not equal to 11 so the answer is not A.
Option B:
First term, \textcolor{blue}{n=1}: 4 \times 1 + 3 = 7 correct for the first term.
Second term, \textcolor{blue}{n=2}: 4 \times 2 + 3 = 11 correct for the second term.
Third term, \textcolor{blue}{n=3}: 4 \times 3 + 3 = 15 correct for the third term.
Fourth term, \textcolor{blue}{n=4}: 4 \times 4 + 3 = 19 correct for fourth term.
Therefore, we can conclude that option B is the correct answer. As practice you could go through the other options with your child to show that they aren’t correct.
Question 3: Polly has \pounds 8 and Norman has \pounds 34.
Norman gives Polly some of his money.
Now, Norman has double the amount of money that Polly has.
How much money did Norman give to Polly?
[3 marks]
First, we need to form an algebraic expression that represents the information in the question.
Once Norman has given Polly the money she will have:
8 + x pounds, where x is the unknown value of money Norman has given to Polly.
Similarly after Norman has given Polly the money he will have:
34 - x pounds, where x is still the amount of money Norman has given to Polly.
After the money has been given, we know that Norman has 2 times the amount of money Polly has.
So, the equation we can form is:
2(8 + x) = 34 - x
This shows that if you multiply the amount of money Polly now has by 2, it will equal the amount of money Norman has.
Now, we can solve the equation to find out how much money Norman gave to Polly.
First, multiply everything in the bracket by \textcolor{darkturquoise}{2}.
16+2x = 34 - x
Now, add \textcolor{darkturquoise}{x} to both sides.
16 + 3x = 34
Then, subtract \textcolor{darkturquoise}{16} from both sides.
3x = 18
Finally divide by \textcolor{darkturquoise}{3}.
x=\pounds 6

