Angles
Angles
Angles are measured using degrees (°).
Your child will need to know the different types of angles, and may also be asked to work out a missing angle on a diagram using angle rules.
Types of Angle
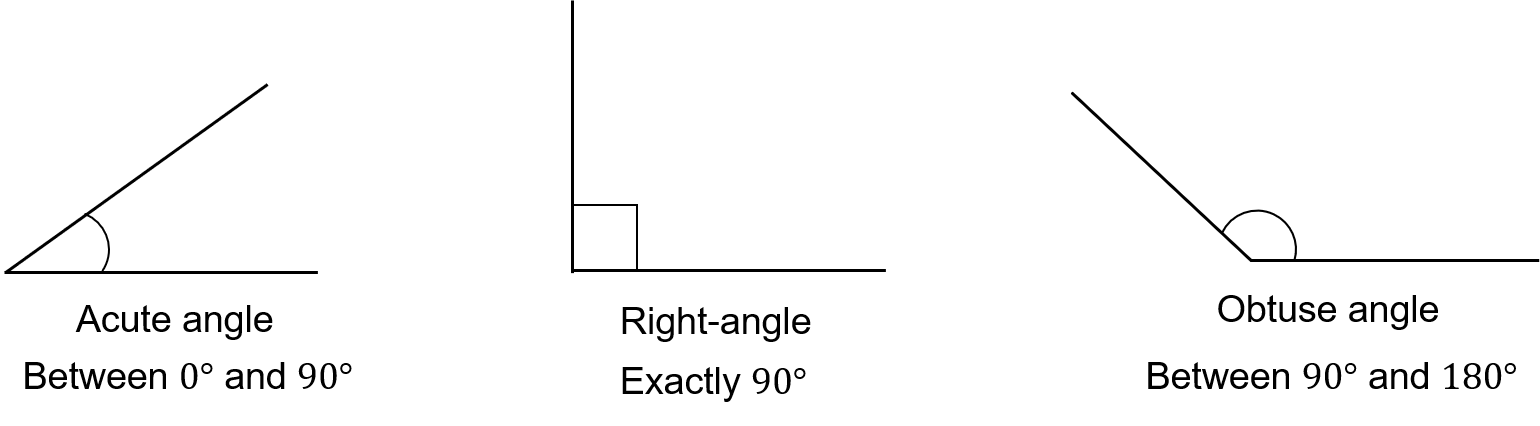
There are three types of angle your child needs to know:
- An acute angle measures between \bf{0°} and \bf{90°}
- A right-angle measures exactly \bf{90°}, and is shown by a square symbol on a diagram.
- An obtuse angle measures between \bf{90°} and \bf{180°}
Angle Rule \bf{1}
Angles around a point add up to \bf{360°}


Example: Find the value of angle x in the diagram.
All the angles around a central point must add up to 360°
The angles we are given so far add up to 100+45+75=220°
So angle x must be 360-220=140°
Angle Rule \bf{2}
Angles on a straight line add up to \bf{180°}


Example: Find the value of angle a in the diagram.
All the angles on a straight line must add up to 180°
The angle we are given is 150°
So angle a must be 180-150=30°
Angle Rule \bf{3}
Angles in a triangle add up to \bf{180°}


Example: Find the value of angle p in the diagram.
All three angles in the triangle must add up to 180°
The angles we are given so far add up to 25+80=105°
So angle p must be 180-105=75°
Angle Rule \bf{4}
Angles in a quadrilateral add up to \bf{360°}


Example: Find the value of angle f in the diagram.
All four angles in the quadrilateral must add up to 360°
The angles we are given so far add up to 125+80+52=257°
So angle f must be 360-257=103°
Example: Finding Missing Angles in a Composite Shape
A composite shape is made up of smaller shapes. Your child may have to use more than one rule to find a missing angle in a composite shape.
Example: Find the values of:
a) Angle a
b) Angle b
c) Angle c

a) The left hand shape is a quadrilateral, and we know the angles in a quadrilateral add up to 360°
The angle with the square symbol must be a right-angle, which is 90°
So we know three angles in the quadrilateral. They add up to 90+68+80=238°
So angle a must be 360-238=122°
b) We know angles on a straight line add up to 180°
We also know that angle a=122°
So angle b must be 180-122=58°
c) The right hand shape is a triangle, and we know the angles in a triangle add up to 180°
We also know that angle b=58°
So we know two angles in the triangle. They add up to 72+58=130°
So angle c must be 180-130=50°
Angles Example Questions
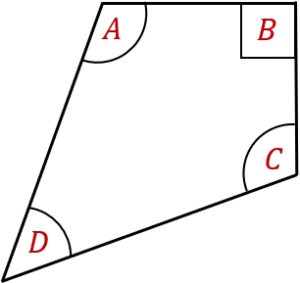
Question 1: Which angle on the shape below is acute?
[1 mark]
An acute angle is bigger than 0° but smaller than 90°, so must be angle D.
Question 2: Find the value of angle x on the diagram.
 [1 mark]
[1 mark]
Angles on a straight line add up to 180°, so x=180-55=125°
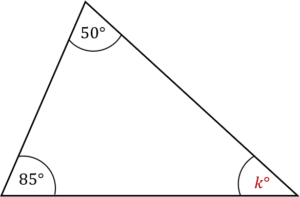
Question 3: Find the value of angle k on the diagram.
[1 mark]
Angles in a triangle add up to 180°
The two angles we know add up to 50+85=135°
So k=180-135=45°
Question 4: What is the size of the angle marked x between the hands on this clock?

[3 marks]
The angle around the centre point of the clock is 360°
We know there are 12 hours equally spaces around the clock, so the angle between each hour must be 360\div12=30°
The hands are 4 hours apart.
So the angle between them must be 4\times30°=120°
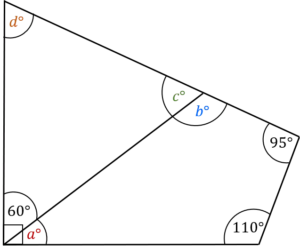
Question 5: Find the values of:
a) angle a
b) angle b
c) angle c
d) angle d
[4 marks]
a) The angle with a square symbol is a right-angle, which is 90°
So a=90-60=30°
b) The right hand shape is a quadrilateral, and we know the angles in a quadrilateral add up to 360°.
We know three of the angles in the quadrilateral, which add up to 30+110+95=235°.
So b=360-235=125°
c) We know angles on a straight line add up to 180°, so c=180-125=55°
d) The left hand shape is a triangle, and we know the angles in a triangle add up to 180°
We know two of the angles in the triangle, which add up to 60+55=115°
So d=180-115=65°

