Fractions
Fractions
Fractions are parts of a whole number. They have a numerator (the top number) and a denominator (the bottom number). A good thing for your child to remember is the line of a fraction just means division.
For their exam your child will need to know how to add, subtract, multiply and divide fractions.
What is a Fraction?
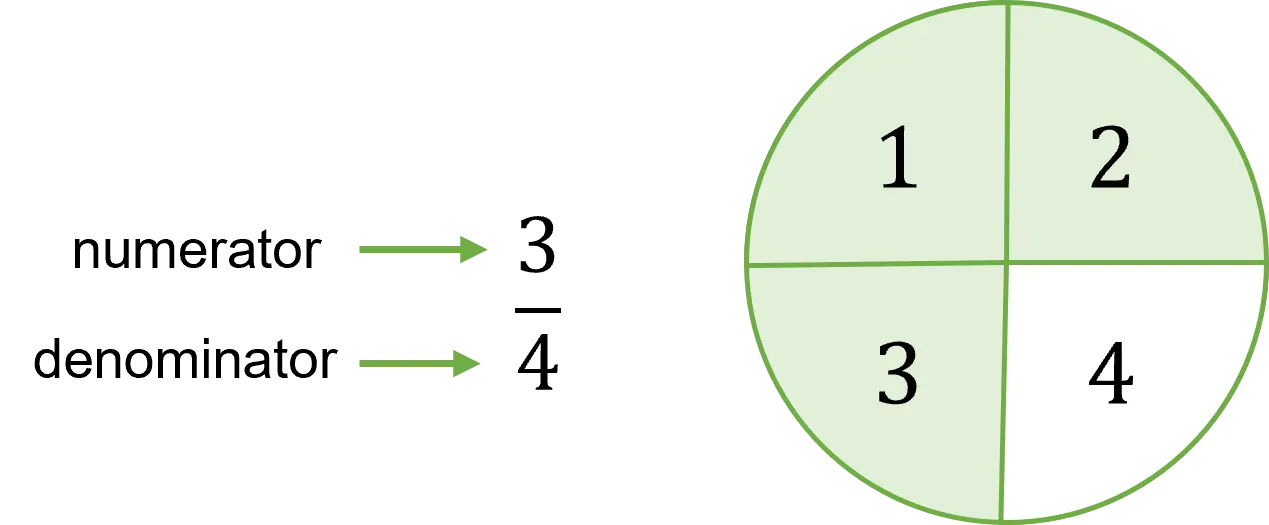
A fraction is part of a whole number. The denominator tells your child how many parts the whole number has been cut into and the numerator indicates how many parts we have.
In the example, the circle represents the whole which is cut up into \textcolor{darkturquoise}{4} equal parts.
The numerator then tells us \textcolor{darkturquoise}{3} of the parts are shaded in.
To help your child understand fractions, go through the following examples of finding fractions of amounts.
Example 1: Fractions of an Amount
To find the fraction of an amount, divide the number by the denominator then multiply by the numerator.
a) What is \dfrac{2}{3} of 18?
b) What is \dfrac{4}{9} of 36?
c) What is \dfrac{5}{7} of 56?
[3 marks]
a) The numerator is \textcolor{orange}{2}
The denominator is \textcolor{purple}{3}
18 \textcolor{purple}{\div 3} \textcolor{orange}{\times 2} =12
b) The numerator is \textcolor{orange}{4}
The denominator is \textcolor{purple}{9}
36 \textcolor{purple}{\div 9} \textcolor{orange}{\times 4} = 16
c) The numerator is \textcolor{orange}{5}
The denominator is \textcolor{purple}{7}
56 \textcolor{purple}{\div 7} \textcolor{orange}{\times 5} = 40
Equivalent Fractions
Equivalent fractions are fractions that are equal but have different numerators and denominators.
Example: What is the simplest equivalent fraction to \dfrac{2}{8} ?
First, find the greatest number that divides into both the numerator and the denominator. In this case both 2 and 8 are divisible by 2.
Divide the numerator and denominator by \textcolor{red}{2}.
\dfrac{2 \textcolor{red}{\div 2}}{8 \textcolor{red}{\div 2}} = \dfrac{1}{4}
Example: What is the simplest equivalent fraction to \dfrac{27}{63} ?
Both the numerator and denominator are divisible by 9.
Divide the numerator and denominator by \textcolor{red}{9}.
\dfrac{27 \textcolor{red}{\div 9}}{63 \textcolor{red}{\div 9}} = \dfrac{3}{7}
Improper Fractions
Your child may come across improper fractions in their revision and exams. Improper fractions have a numerator that is greater than the denominator and this indicates that the number is greater than \bold{\textcolor{red}{1}}.
Mixed numbers are another way of expressing a fraction that is greater than \bold{\textcolor{red}{1}}. Your child may be asked to convert between improper fractions and mixed numbers.
Example: Convert \dfrac{13}{5} into a mixed number.
\dfrac{13}{5} = 13 \div 5
First, find how many whole times 5 goes into 13.
13 \div 5 = \textcolor{green}{2} r \textcolor{purple}{3}
The mixed number can then be found by writing the number of whole times 5 goes into 13 as a big number at the front.
Then, the remainder of the calculation as the numerator of the fraction with the denominator staying as 5.
So, the answer becomes:
\dfrac{13}{5} = \textcolor{green}{2} \dfrac{\textcolor{purple}{3}}{5}
Adding and Subtracting Fractions
If two fractions have the same denominator or common denominator, then adding and subtracting is simple.
Add or subtract the numerators and keep the denominators the same.
Example: \dfrac{7}{\textcolor{red}{9}} - \dfrac{2}{\textcolor{red}{9}}
The denominator of both fractions are the same, in order to subtract the fractions, your child needs to subtract one numerator from the other.
\dfrac{7}{\textcolor{red}{9}} - \dfrac{2}{\textcolor{red}{9}} = \dfrac{7 - 2}{\textcolor{red}{9}}=\dfrac{5}{\textcolor{red}{9}}
When the denominators are different, your child needs to use their skills of finding equivalent fractions to make the denominators the same.
Example: \dfrac{3}{5} + \dfrac{4}{15}
In this example, the denominators are different so multiply the numerator and the denominator of \dfrac{3}{5} by \textcolor{red}{3}.
\dfrac{3}{5} \times \textcolor{red}{\dfrac{3}{3}} = \dfrac{9}{15}
Now the fractions both have a denominator of 15 so they can be added as normal.
\dfrac{9}{15} + \dfrac{4}{15} = \dfrac{13}{15}
Multiplying Fractions
Multiplying fractions by whole number:
In their exam your child may be asked to multiply a fraction by a whole number. In order to do that, multiply the numerator by the whole number and leave the denominator as it is.
Example: \dfrac{3}{11} \times 5
The numerator is 3
\dfrac{3 \times 5}{\textcolor{purple}{11}} = \dfrac{15}{\textcolor{purple}{11}}
Multiplying fractions by another fraction:
When multiplying a fraction by another fraction your child needs to multiply the numerators together and multiply the denominators together.
Example: \dfrac{6}{7} \times \dfrac{5}{8}
Multiply the numerators and denominators together.
\dfrac{\textcolor{orange}{6}}{\textcolor{purple}{7}} \times \dfrac{\textcolor{orange}{5}}{\textcolor{purple}{8}} = \dfrac{\textcolor{orange}{6 \times 5}}{\textcolor{purple}{7 \times 8}} = \dfrac{30}{56}
The fraction \dfrac{30}{56} can be simplified by finding an equivalent fraction.
30 and 56 both divide by 2 so simplify the fraction by dividing the numerator and denominator by 2.
\dfrac{30 \textcolor{red}{\div 2}}{56 \textcolor{red}{\div 2}} = \dfrac{15}{28}
Dividing Fractions by Whole Numbers
When dividing fractions by a whole number, your child needs to multiply the denominator by the whole number.
Example: \dfrac{5}{12} \div 6
The denominator is \textcolor{purple}{12} so to find the new denominator, multiply \textcolor{purple}{12} by \textcolor{red}{6}.
So, the calculation becomes:
\dfrac{5}{\textcolor{purple}{12}} \textcolor{red}{\div 6} = \dfrac{5}{\textcolor{purple}{12} \textcolor{red}{\times 6}} = \dfrac{5}{72}
Fractions Example Questions
Question 1: Put these fractions in order from smallest to largest.
\dfrac{2}{3},\,\,\dfrac{7}{8},\,\,\dfrac{5}{6},\,\,\dfrac{7}{12}
[1 mark]
In order to answer questions like this, your child needs to be able to convert the fractions into equivalent fractions. This is so the fractions have a common denominator and are easier to compare.
Any common multiple of the denominators would work for the common denominator but the smallest common multiple is 24.
For \dfrac{2}{3}: multiply the numerator and denominator by \textcolor{red}{8}
\dfrac{2\textcolor{red}{\times 8}}{3\textcolor{red}{\times 8}} = \dfrac{16}{24}
For \dfrac{7}{8}: multiply the numerator and denominator by \textcolor{red}{3}
\dfrac{7 \textcolor{red}{\times 3}}{8 \textcolor{red}{\times 3}} = \dfrac{21}{24}
For \dfrac{5}{6}: multiply the numerator and denominator by \textcolor{red}{4}
\dfrac{5 \textcolor{red}{\times 4}}{6 \textcolor{red}{\times 4}} = \dfrac{20}{24}
For \dfrac{7}{12}: multiply the numerator and denominator by \textcolor{red}{2}
\dfrac{7 \textcolor{red}{\times 2}}{12 \textcolor{red}{\times 2}} = \dfrac{14}{24}
Next, order the fractions based on the numerators.
\dfrac{14}{24},\,\,\dfrac{16}{24},\,\,\dfrac{20}{24},\,\,\dfrac{21}{24}
So, the final order of the fractions is:
\dfrac{7}{12},\,\,\dfrac{2}{3},\,\,\dfrac{5}{6},\,\,\dfrac{7}{8}
Question 2: 
What fraction of the grid is shaded?
Give your answer in its simplest form.
[2 marks]
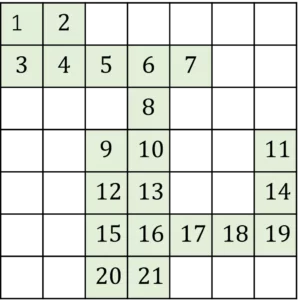
Count the shaded squares, in this case there are \textcolor{green}{21} shaded squares.
In total there are 49 squares. Using these values, form the fraction.
\dfrac{\textcolor{green}{21}}{49}
The question says that the answer needs to be in its simplest form which means we need to find an equivalent form.
Both 21 and 49 are in the 7 times tables so, divide the numerator and denominator by 7.
\dfrac{21 \div 7}{49 \div 7} = \dfrac{3}{7}
Question 3: A pair of trousers has the original price of £24. Bobby buys the trousers when they are the sale with a \dfrac{1}{4} off the original price.
How much did Bobby pay for the trousers?
[2 marks]
To find \dfrac{1}{4} of £24, divide by \textcolor{red}{4}.
£24 \textcolor{red}{\div 4} = £6
Then, to find the sales price subtract the discount off the original price.
£24 - \textcolor{red}{£6} = £18

