Fractions, Decimals and Percentages
Fractions, Decimals and Percentages
Fractions, decimals and percentages are different ways of expressing the same thing. In different contexts, different expressions may be more helpful. Converting between fractions, decimals and percentages is an important skill for your child to develop as well as how to tackle exam questions that may involve all three.
Converting from Decimals to Percentages
There is a rule that is easy to remember for converting between decimals and percentages.
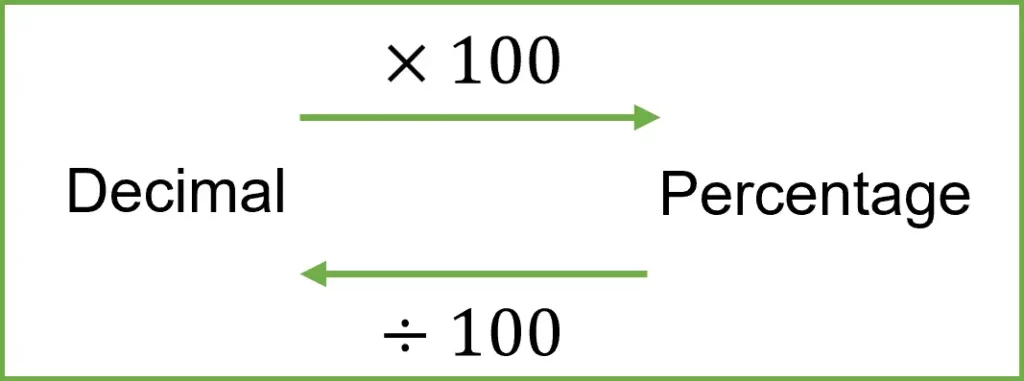

Example: Convert 0.55 to a percentage.
Using the rule, follow the arrow from decimal to percentage to see we need to multiply 0.55 by 100.
0.55 \textcolor{green}{\times 100} = 55\%
Example: Convert 75\% to a decimal.
This time using the rule follow the arrow from percentage to decimal to find we need to divide by 100.
75\% \textcolor{green}{\div 100} = 0.75
Converting Fractions into Percentages
For fractions that have \textcolor{blue}{100} as their denominator, the equivalent percentage is the value of the numerator.
Example: Find \dfrac{85}{100} as a percentage.
\textcolor{blue}{100} is the denominator so, the equivalent percentage is \textcolor{purple}{85\%}.
Your child may come across fractions that don’t have a denominator of \textcolor{blue}{100}. In these cases they need to find an equivalent fraction that does have a denominator of \textcolor{blue}{100} and then the numerator of that fraction will be the percentage.
Example: Convert \dfrac{7}{20} into a percentage.
As the denominator does not equal \textcolor{blue}{100}, find an equivalent fraction to \dfrac{7}{20} that has the denominator of \textcolor{blue}{100}.
100 = 20 \textcolor{red}{\times 5}
So, multiply the numerator by \textcolor{red}{5} as well to form the equivalent fraction.
7 \textcolor{red}{\times 5} = 35
So,
\dfrac{7}{20} = \dfrac{\textcolor{purple}{35}}{\textcolor{blue}{100}}
Now, it’s easy to see that \dfrac{7}{20} as a percentage is \textcolor{purple}{35\%}.
To convert the opposite way from percentage to fraction, put the percentage as the numerator and the denominator as \textcolor{blue}{100}. Then, simplify the fraction if necessary.
Example: Convert 45\% to a fraction and simplify it.
Put the percentage as the numerator and \textcolor{blue}{100} as the denominator.
\dfrac{45}{100}
This can be simplified as both 45 and 100 are divisible by \textcolor{red}{5}.
\dfrac{45 \textcolor{red}{\div 5}}{100 \textcolor{red}{\div 5}} = \dfrac{9}{20}
Converting Fractions into Decimals
Similar to when your child converts fractions to percentages, converting from fractions to decimals involves finding an equivalent fraction with a denominator of \textcolor{blue}{100}.
Example: Convert \dfrac{3}{25} into a decimal.
First, find an equivalent fraction with a denominator of \textcolor{blue}{100}.
\dfrac{3 \textcolor{red}{\times 4}}{25 \textcolor{red}{\times 4}} = \dfrac{12}{100}
Then, to find the fraction as a decimal it’s important for your child to remember that the line in a fraction just means ‘divide’.
So, the calculation to find the decimal becomes:
12 \div 100 = 0.12
Converting from a decimal to a fraction is the same process in reverse.
Example: Convert 0.92 into a fraction.
Start by multiplying the decimal by \textcolor{darkturquoise}{100}, your child may remember that this is how to convert a decimal to a percentage.
0.92 \times 100 = 92\%
Then, put this number as the numerator of a fraction with the denominator as \textcolor{blue}{100}.
\dfrac{92}{100}
This fraction can be left as it is or simplified, your child should be aware from the question how they should express their answer.
Fractions, Decimals and Percentages Example Questions
Question 1: Convert the following into fractions in their simplest form.
a) 0.34
b) 55\%
c) 0.03
[3 marks]
a) First multiply the decimal by 100
0.34 \times 100 = 34
Then use that number as the numerator of a fraction, with the denominator of \textcolor{blue}{100} and simplify.
\dfrac{34}{100} = \dfrac{34 \textcolor{red}{\div 2}}{100 \textcolor{red}{\div 2}} = \dfrac{17}{50}
b) Put 55 as the numerator and 100 as the denominator of the fraction.
\dfrac{55}{100}
Then, simplify the fraction by finding an equivalent fraction.
\dfrac{55 \textcolor{red}{\div 5}}{100 \textcolor{red}{\div 5}} = \dfrac{11}{20}
c) First, multiply the decimal by 100.
0.03 \times 100 = 3
Put that number as the numerator of a fraction with the denominator of \textcolor{blue}{100}.
\dfrac{3}{100}
This fraction cannot be simplified so this is our final answer.
Question 2: What percentage of the triangles are shaded?
[2 marks]

First count how many shaded triangles there are:
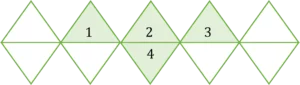
There are 4 shaded triangles and 10 triangles altogether.
Next, form a fraction using this information.
\dfrac{4}{10} of the triangles are shaded.
Then, find an equivalent fraction with the denominator of \textcolor{blue}{100}.
\dfrac{4 \textcolor{red}{\times 10}}{10 \textcolor{red}{\times 10}} = \dfrac{40}{100}
Finally, the percentage is the numerator of the fraction we have found.
40\% of the triangles are shaded.
Question 3: Caroline, Kevin and Vinny share a house.
Caroline pays \dfrac{1}{4} of the rent, Kevin pays 50\% of the rent and Vinny pays \pounds 350.
How much do they pay for the total rent of their house?
[3 marks]
First, convert \dfrac{1}{4} into a percentage.
\dfrac{1 \textcolor{red}{\times 25}}{4 \textcolor{red}{\times 25}} = \dfrac{25}{100} = \textcolor{green}{25\%}
So, Caroline pays 25\% of the rent.
Together, Caroline and Kevin pay 50\% + 25\% = 75\% of the rent.
The total rent is represented by 100\% so, Vinny pays 100\% - 75\% = 25\% of the rent.
As we know how much Vinny pays, we can work out the total rent.
\textcolor{purple}{25\%} \textcolor{red}{\times 4} = \textcolor{orange}{100\%}
\textcolor{purple}{\pounds 350} \textcolor{red}{\times 4} = \textcolor{orange}{\pounds 1400}
So, the total rent paid is \pounds 1400.

