Number Basics
Number Basics
There are many different types of numbers that you and your child may come across when revising and it’s important that you can recognise properties of numbers. These types of numbers include odd and even numbers, negative numbers, whole numbers, prime numbers and square numbers.
Even or Odd Numbers
A whole number can either be odd or even.
An even number is a whole number that can be divided by 2. For example 8 is an even number as 8 \div 2 = 4 which is a whole number.
An odd number is a whole number that can’t be divided by 2. For example 5 is an odd number as 5 \div 2 = 2.5 which is not a whole number.
Positive and Negative Numbers
Numbers can also be either positive, if they are greater than 0 or negative, if they are less than 0.
A number line can be used to help visualise the difference between positive and negative numbers.
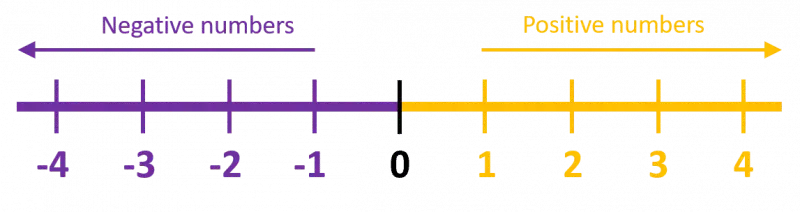
On the left of the number line you can see the negative numbers and on the right you can see the positive numbers. Number lines can be used to show how big a number is in comparison to another number.
On the number line above 4 is the biggest number and -4 is the smallest number.
Factors and Multiples
A factor of a number is a whole number that divides into that number.
A question may ask your child to find common factors of two numbers. This can be done by listing the factors of both numbers and identifying numbers that appear in both lists.
A multiple of a number is found by multiplying a whole number by another whole number. The exam may ask your child to find common multiples of 2 whole numbers. In a similar way to finding common factors, common multiples can be found by listing multiples of each number and identifying numbers that appear on both lists.
Example 1: Common Factors
Find the common factors of 30 and 20.
[1 mark]
Factors of 30:\,1,\,2,\,3,\,5,\,6,\,10,\,15,\,30
Factors of 20:\,1,\,2,\,4,\,5,\,10,\,20
Common factors of 30 and 20 are numbers that are found in both lists.
Common factors are 1,\,2,\,5,\,10
Prime Numbers
Prime numbers have exactly two factors, 1 and themselves.
For example 11 is a prime number as the only whole numbers that divide into it are 1 and 11.
- 1 is not a prime number as it only has one factor.
- The smallest prime number and only even prime number is 2.
- The ten smallest prime numbers are: 2,\,3,\,5,\,7,\,11,\,13,\,17,\,19,\,23 and 29.
Square and Cube Numbers
If you multiply a whole number by itself then you get a square number. There are a few different ways that square numbers can be written.
For example 5 squared or 5 \times 5 =25, so 25 is a square number.
Some handy notation that you might see uses indices to write square numbers e.g. 5 \times 5 = 5^{2} , as shown this is still equal to 25.
Cube numbers are similar to square numbers except a whole number is multiplied by itself twice.
For example 3 cubed would be 3 \times 3 \times 3 = 27 so 27 is a cube number. Similar notation can be used to express cube numbers e.g. 3 \times 3 \times 3 = 3^{3}
Roman Numerals
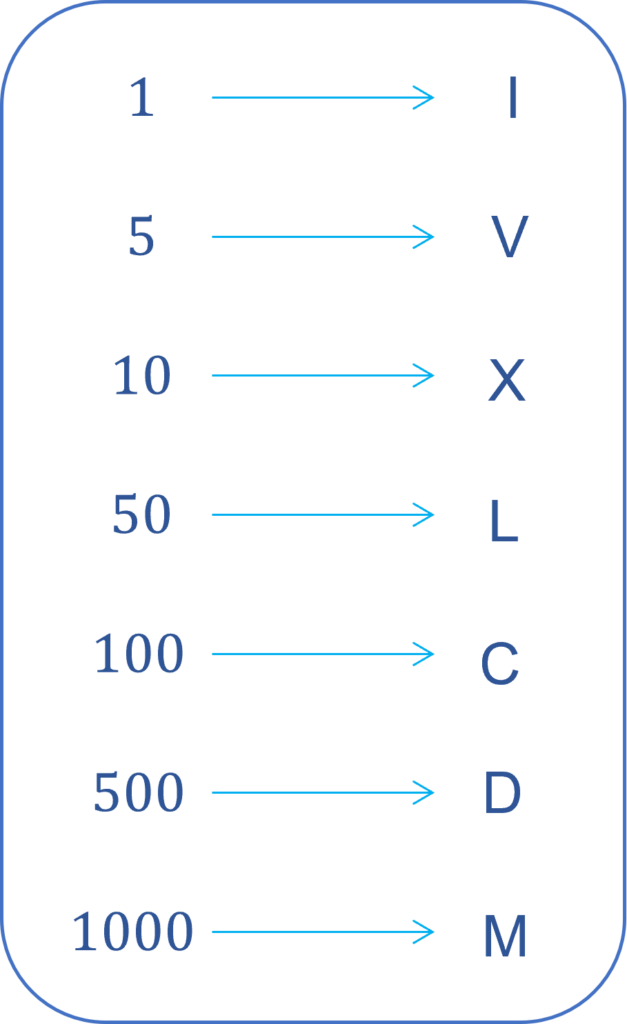
Roman numerals use letters that represent certain numbers and are then used to make up all of the other numbers.
The Roman numerals that your child is expected to be familiar with are seen to the right.
Some numbers are added together to produce higher numbers.
For example 3 = 1 + 1 + 1 = III in Roman numerals and 11 = 10 + 1 = XI in Roman numerals.
Other numbers are represented as subtractions if they are 9s or 4s.
For example 19 = 10 + 10 - 1 = IXX.
Commonly years are represented by Roman numerals so it is important your child is comfortable representing higher numbers in Roman numerals.
Example 2: Writing years as Roman numerals
a. Write the year 1529 in Roman numerals.
[1 mark]
1000 + 500 + 10 + 10 + 10 - 1 = 1529MDXXIX
b. Write the number MCMXVIII in digits.
[1 mark]
MCM =1000 + 1000 - 100 = 1900
XVIII =10 + 5 + 1 + 1 + 1 = 18
So, putting them together MCMXVIII =1900 + 18 = 1918
Number Basics Example Questions
Question 1: Sort the following numbers into the table.
1,\,2,\,3,\,4,\,5,\,6,\,7,\,8,\,9,\,10[1 mark]

Remember, 2 is the only even prime number, so is the only number in that section of the table. 
Question 2: Using the number line, find the difference between -2 and 3.

[1 mark]

As shown on the number line above, there are 5 jumps between -2 and 3. Therefore the difference between -2 and 3 is 5.
Question 3: What is the sum of the prime numbers between 1 and 10?
[1 mark]
The prime numbers between 1 and 10 are:
2,\,3,\,5 and 7
Add these numbers together to work out the sum.
2 + 3 + 5 + 7 = 17

