Ratio and Proportion
Ratio and Proportion
Ratios are used to compare how much of one thing there is in comparison to how much of another thing there is. Proportion is a similar concept but is used to compare how much of one thing there is in comparison to the whole.
These concepts can be tricky for your child to get to grips with as they are similar. Work through these examples with your child to help familiarise them with the concepts.
Ratio


A ratio is a written as \bold{\textcolor{green}{1:4}} and is said ‘one to four’.
This is a ratio in its simplest form as there is no number that will divide into both numbers.
To form a ratio of purple circles to red triangles count the respective shapes in the image.

There are 8 purple circles and 2 red triangles.
Now, you can help your child to form the ratio of circles to triangles.
\textcolor{purple}{8}:\textcolor{red}{2}
Unlike the previous example this ratio is not in its simplest form. Both values can be divided by 2, so if we divide both sides of the ratio by 2, we can find the ratio in its simplest form.
\textcolor{purple}{8} \div 2 : \textcolor{red}{2} \div 2
\textcolor{purple}{4} : \textcolor{red}{1}
Looking back at the image, we can group the shapes to see that there is 4 purple circles then 1 red triangle.

So, you can see that for every 4 purple circles there is 1 red triangle. This is the information that the ratio is telling us.
Example 1: Ratio
Nigel and Sally split up some prize money.
Nigel gets \pounds 90 and Sally gets \pounds 150.
What is the ratio of the amount of money Nigel gets to the amount of money Sally gets in its simplest form?
[2 marks]
First, form the initial ratio with the values in the question.
\pounds 90 : \pounds 150
Divide both values by \textcolor{red}{10} to begin to simplify the ratio.
90 \textcolor{red}{\div 10} : 150 \textcolor{red}{\div 10}
9 : 15
This ratio can be simplified further as both values are divisible by \textcolor{red}{3}.
9 \textcolor{red}{\div 3} : 15 \textcolor{red}{\div 3}
3 : 5
Now, the ratio is in its simplest form and this is our final answer.
Proportion
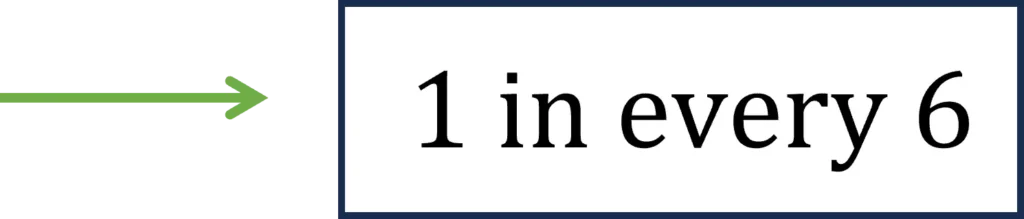
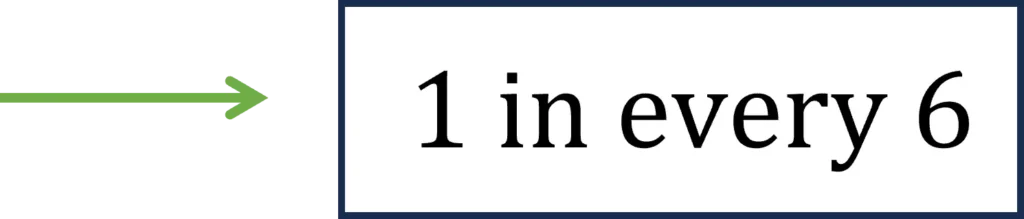
Proportion refers to how much of one thing there is in comparison to the whole. In the example to the right, the 6 refers to the whole and of those 6 one of them has a certain property.
Proportional statements convey the same information as a fraction. The statement 1 in every 6 is the same as saying \dfrac{1}{6}.
Example: The proportion of blue squares in the image below is 1 in 6
This is the same as saying \dfrac{1}{6} of the squares are blue.

This example demonstrates to your child how ratio and proportion are different. The proportional statements informs us that for every 6 squares, 1 of them is blue.
The ratio will tell us how many blue squares there are in comparison to the number of green squares.
The ratio of blue squares to green squares is \textcolor{blue}{1} : \textcolor{green}{ 5}.
Example 2: Proportion
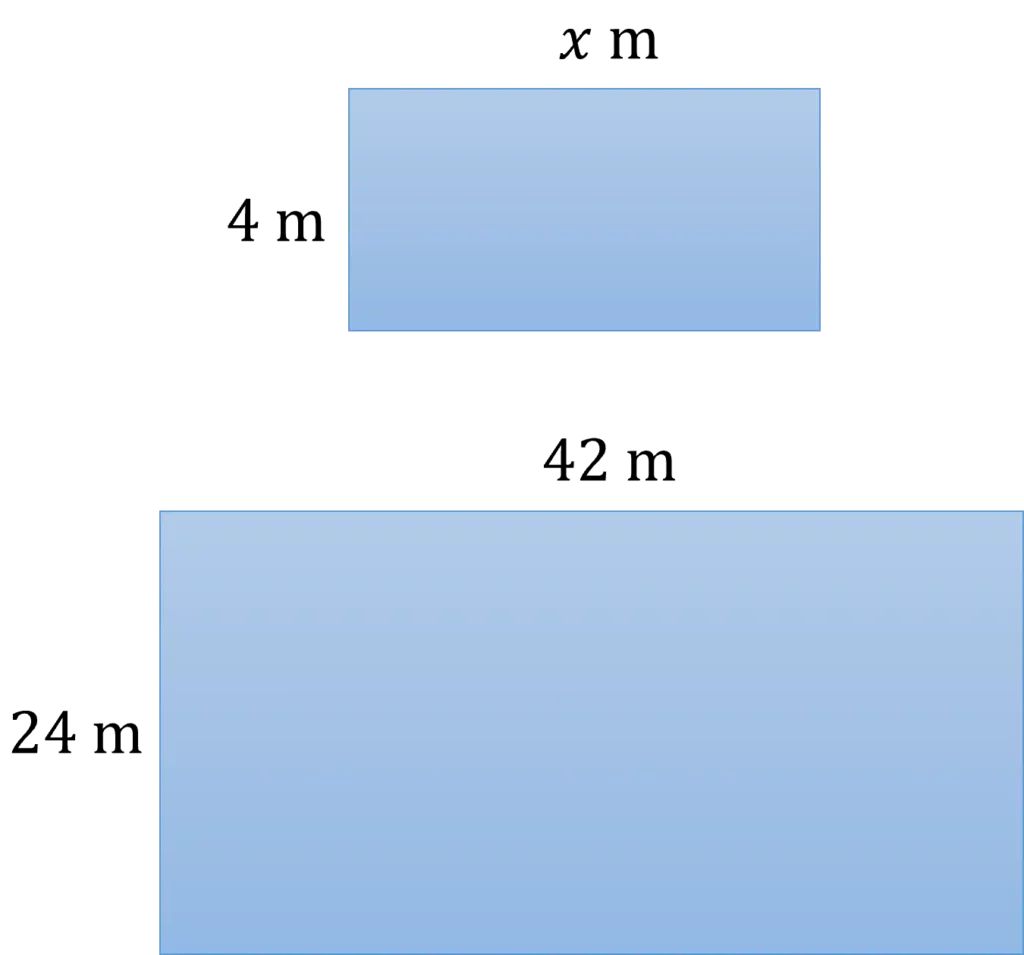

Your child may come across similar shapes in relation to ratio. To get the side lengths of the bigger shape multiply by a number called the scale factor. This can then be used to find the ratio between the sides of the shape.
Example: The two rectangles on the right hand side are similar shapes.
a) Find the ratio between the pairs of sides of the the rectangles.
b) Find the value of x
a) The pair of sides labelled 4\text{ m} and 24\text{ m} can be written as a ratio then simplified.
4 : 24
Both of the numbers are divisible by \textcolor{red}{4}.
4 \textcolor{red}{\div 4} : 24 \textcolor{red}{\div 4} = 1 : 6
The ratio 1:6 can’t be simplified further so, it is the ratio in its simplest form.
b) Now, using the ratio we can apply it to the other pair of sides to find x\text{ m}.
1:6
Substituting in the values for the other pair of sides we see that the ratio becomes:
x : 42
By finding the scale factor from the simplified ratio to the newly formed ratio, we can find the value of x.
Scale factor: 42 \div 6 = \textcolor{red}{7}
Now applying the scale factor, we can find x\text{ m}.
x = 1 \textcolor{red}{\times 7} = 7
7 : 42
Ratio and Proportion Example Questions
Question 1: Divide the following numbers into the ratios.
a) 400 in the ratio 2:3
b) 350 in the ratio 4:3
[4 marks]
a) Total parts in the ratio = 2+3 = 5
One part of the ratio will equal 400 \div 5 = 80
2 parts = 80 \times 2 = 160
3 parts = 80 \times 3 = 240
Split into the ratio the answer is 160 : 240
b) Total parts in the ratio = 4 + 3 =7
One part of the ratio =350 \div 7 = 50
4 parts =50 \times 4 = 200
3 parts = 50 \times 3 = 150
Split into the ratio the answer is 200:150
Question 2: The rectangles below are similar shapes.
Work out the missing length, x on the larger rectangle.
[3 marks]

First, find the scale factor using the pair of sides, 7\text{ m} and 28\text{ m}.
Scale factor = 28 \div 7 = \textcolor{red}{4}
Using the scale factor, find the missing side:
x = 3 \text{ m} \textcolor{red}{\times 4} = 12 \text{ m}
Question 3: Jonathan, Omar and Charlotte share \pounds 96.
Jonathan receives \pounds 30, Omar receives \pounds 24 and Charlotte receives the rest.
Find the ratio of the money received by Jonathan to money received by Omar to money received by Charlotte in its simplest form.
[3 marks]
First, find how much money was received by Charlotte.
\pounds 30 + \pounds 24 = \pounds 54 received by Jonathan and Omar.
Charlotte received \pounds 96 - \pounds 54 = \pounds 42
Next, form the ratio of the money they received.
30: 24: 42
Each of the numbers in the ratios is divisible by 6.
30 \textcolor{red}{\div 6} : 24 \textcolor{red}{\div 6} : 42 \textcolor{red}{\div 6}
So, the final simplified ratio is:
5 : 4 : 7

