Symmetry
Symmetry
Some 2D shapes have a property that they are symmetrical. This means that if they are folded along a line of symmetry the shape will be folded exactly in half. A shape may have multiple lines of symmetry and some have no lines of symmetry at all.
By helping your child through this section, you can help them become more confident with different kinds of symmetry that they may come across in their exam.
Lines of Symmetry
A line of symmetry is the line which splits a shape in half exactly. A shape can have any number of lines of symmetry and it is important that your child learns how to spot how many lines of symmetry a shape has.
Lines of symmetry are also sometimes called mirror lines as they act as a mirror “reflecting” one half of a shape onto the other.
Example:
The trapezium has 1 line of symmetry.
The rectangle has 2 lines of symmetry.
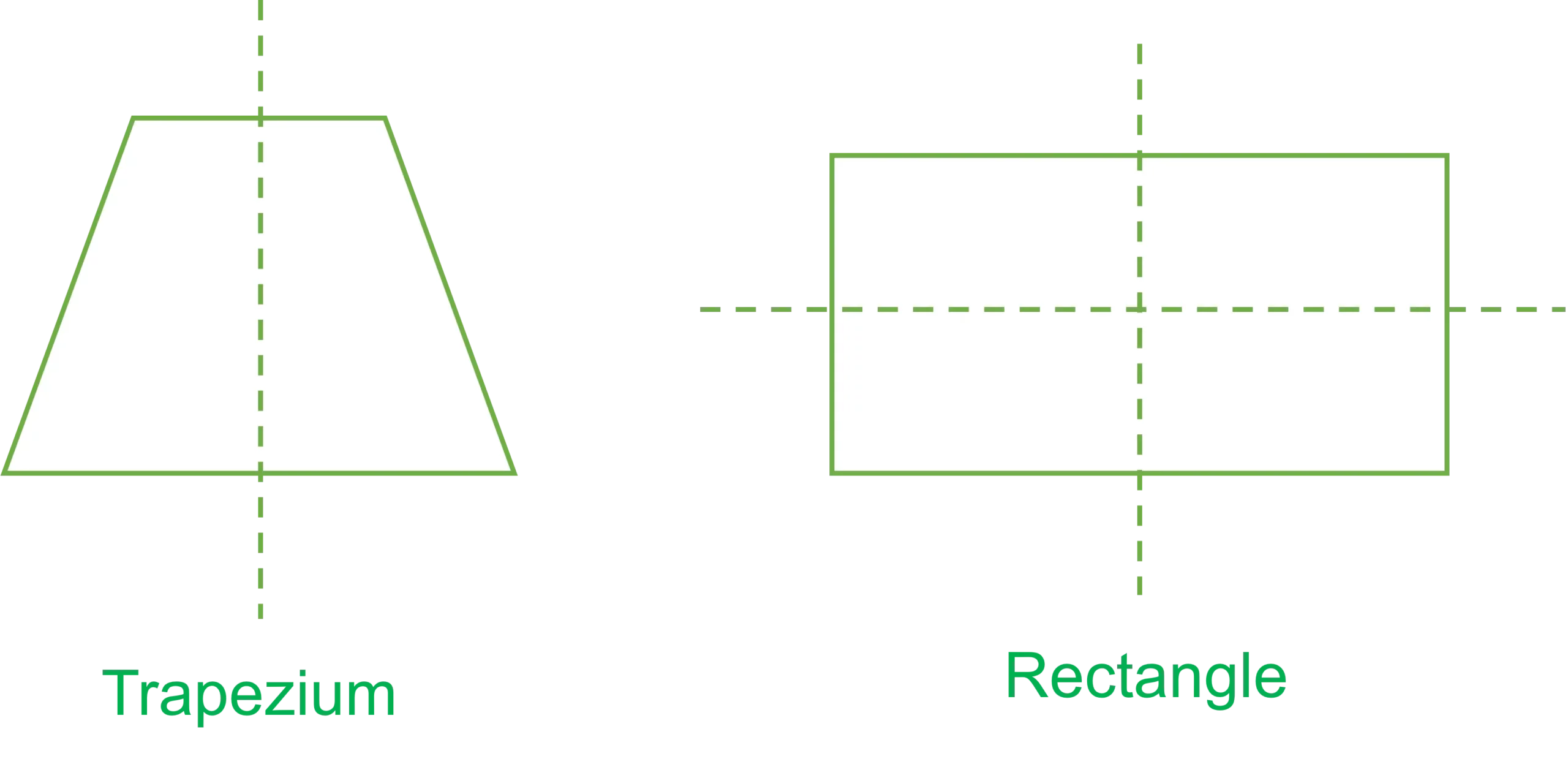
One way your child can get to grips with lines of symmetry is to think about folding paper cut into the shape.
For the rectangle example above, there are two folds that you could make which would fold the piece of paper in half. These two folds are the lines of symmetry.
Example 1: Symmetry
An exam question will often ask your child to find how many lines of symmetry a 2D shape has.
Example: How many lines of symmetry do the following shapes have?

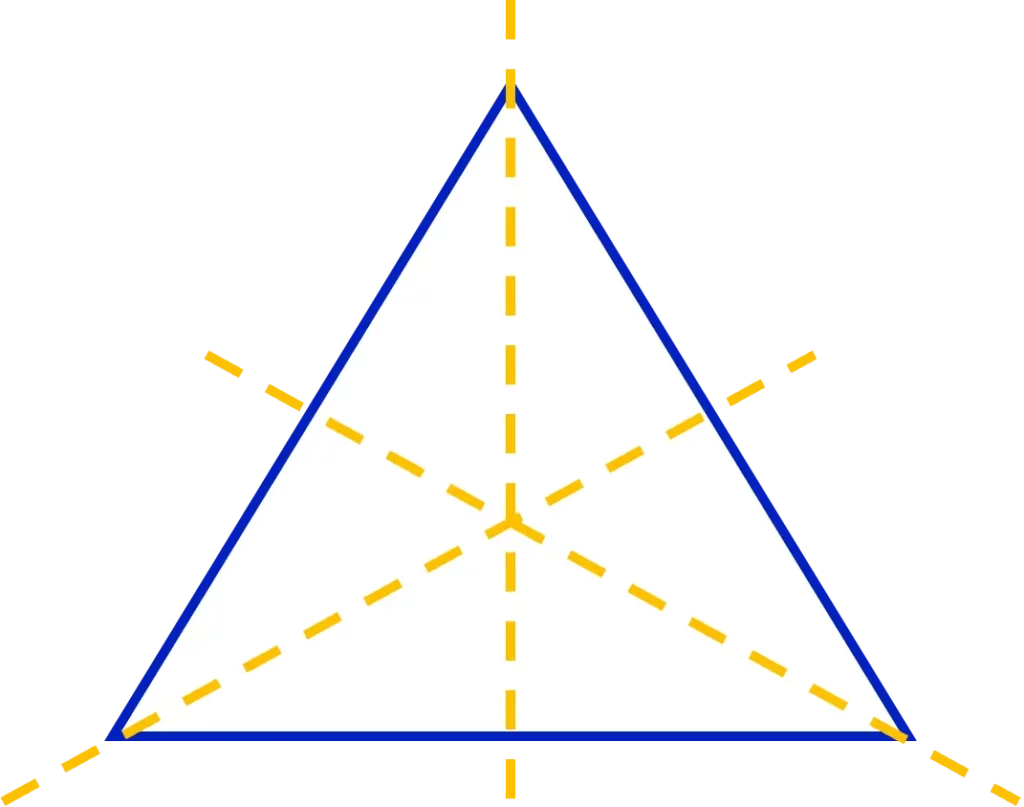

The first shape is an equilateral triangle, there are \bold{\textcolor{darkturquoise}{3}} lines of symmetry.


The next shape can be folded in half along two different lines. So, it has \bold{\textcolor{darkturquoise}{2}} lines of symmetry.
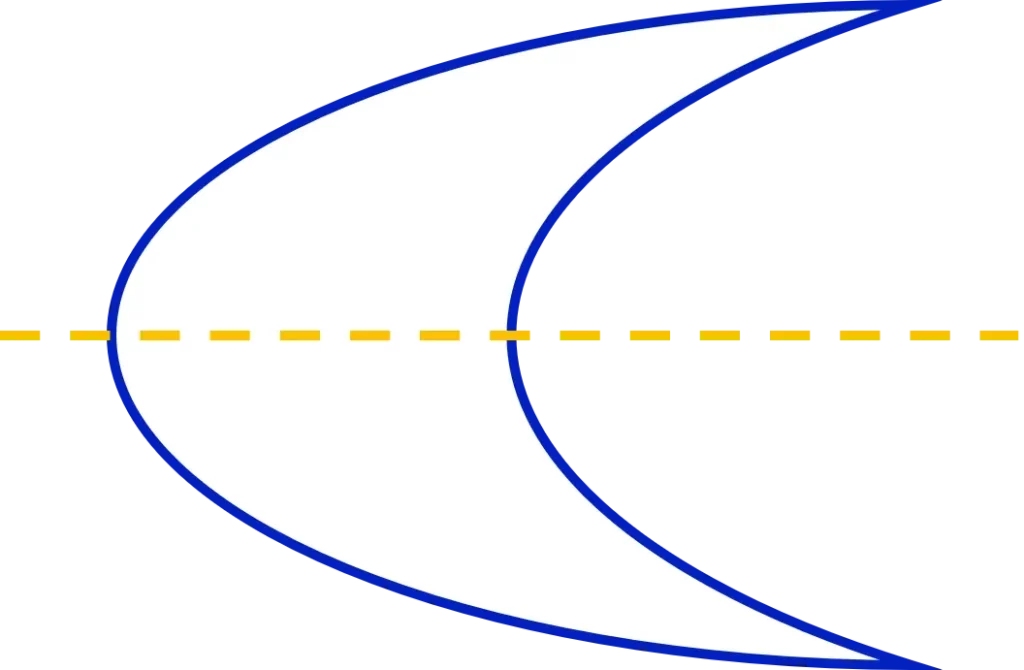

The final shape only has \bold{\textcolor{darkturquoise}{1}} line of symmetry.
Rotational Symmetry
Another type of symmetry that your child needs to be aware of and able to identify is rotational symmetry.
The order of rotational symmetry is how many times a shape looks the same when it is rotated 360\degree around its centre.
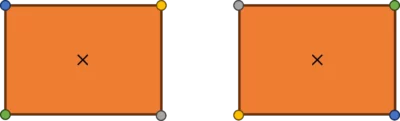
Example: A rectangle has rotational symmetry of order \bold{\textcolor{darkturquoise}{2}} as there are 2 positions where it looks the same when it is rotated.
See below, we have highlighted the corners in different colours to show that the rectangle has been rotated.
All regular polygons, have an order of rotational symmetry equal to the number of sides they have.
For example an equilateral triangle has 3 equal sides and therefore has rotational symmetry of order 3.
Symmetry Example Questions
Question 1: What order of rotational symmetry does the shape below have?
[2 marks]

By adding a green dot to the top of the shape, we can see that the shape has been rotated through 360\degree.
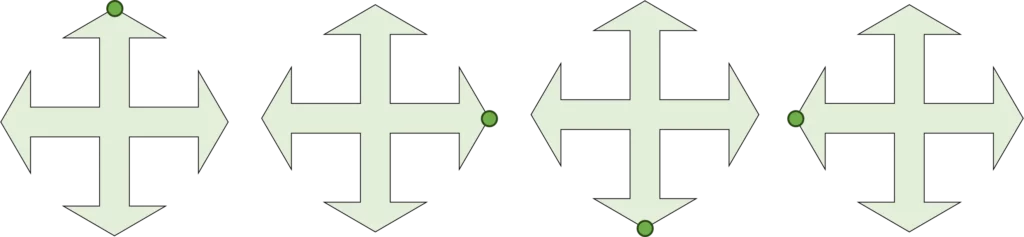
There are four positions of the shape that look the same.
Therefore, this shape has rotational symmetry of order \bold{\textcolor{darkturquoise}{4}}.
Question 2: How many lines of symmetry do the following shapes have?
[2 marks]

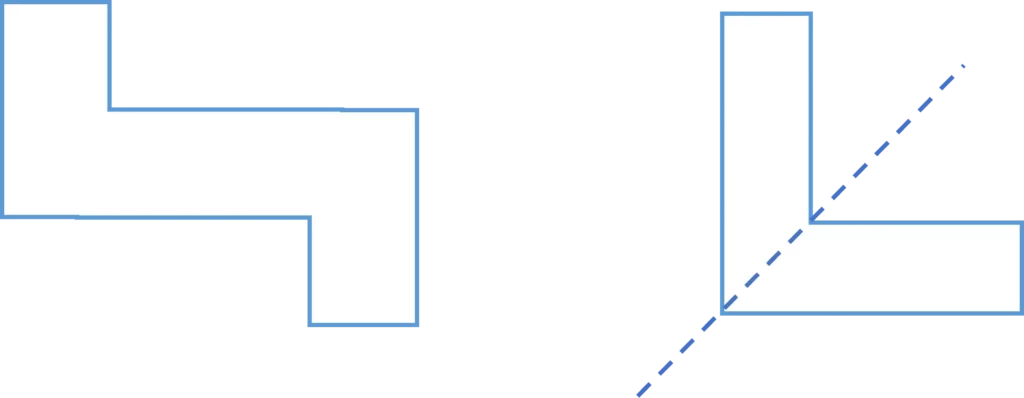
a) This shape doesn’t have any lines of symmetry.
b) This shape has \bold{\textcolor{darkturquoise}{1}} diagonal line of symmetry.
If you had a piece of paper of this shape you could fold it exactly in half along the line shown.
Question 3: What is the order of rotational symmetry for a regular hexagon?
[1 mark]
We know that for regular polygons the order of rotational symmetry is the same as the number of sides that the shape has.
Your child should be able to recall that a hexagon is a \bold{\textcolor{darkturquoise}{6}} sided shape.
So it has rotational symmetry of order \bold{\textcolor{darkturquoise}{6}}.

