Word Problems
Word Problems
Mixed calculations and word problems are more involved questions that your child may encounter in their exam. They may have more context than in some of the practice questions and it might be a bit trickier to work out exactly what the question wants them to do.
Going through the examples on this revision page with your child can help them become familiar with how to spot what the question is asking, so less time in their exam is wasted.
Example 1
Work out 4^{2} + 3(12 - 8)
When there is more than one symbol in a calculation, don’t forget to use BIDMAS.
Brackets: (12-8) = \textcolor{blue}{4}
Remembering that a number in front of a pair of brackets means multiplication, the expression becomes:
4^{2} + 3 \times \textcolor{blue}{4}
Indices: 4^{2} = 4 \times 4 = \textcolor{purple}{16}
So, the expression becomes:
\textcolor{purple}{16} + 3 \times 4
Division: There is no division in this example.
Multiplication: 3 \times 4 = \textcolor{green}{12}
So, we are left with the expression:
16 + \textcolor{green}{12}
Addition: There is only addition left so the final answer is:
16 + 12 = 28
Example 2
Fiona is hosting a party and she needs to buy enough plates for all of her guests.
Fiona expects 201 guests and plates can be bought in packs of 6.
How many packs of plates will Fiona need to buy to make sure there is enough for all the guests?
[2 marks]
To find the number of packs of plates that Fiona needs to buy, we will need to divide the number of guests by the number of plates in one pack.
\textcolor{blue}{201 \div 6 =}


Using the bus stop method for division. The answer to our calculation is:
\textcolor{blue}{201 \div 6 = 33.5}
It is important for your child to do a sense check at this point in the question and not just write \textcolor{blue}{33.5} as the answer.
Fiona can’t buy \textcolor{red}{33.5} packs of plates because this doesn’t make sense.
Fiona can’t buy \textcolor{red}{33} packs as she still wouldn’t have enough for all of her guests.
Therefore, Fiona must buy \textcolor{green}{34} packs of plates in order for no guests to be left out. Even though this means she will have some extra plates.
Example 3
Angelina is painting some wooden blocks for a craft project. All of the blocks are the same size. 3 tins of paint are needed to paint 87 blocks.
How many of the wooden blocks can be painted using 7 tins of paint?
[2 marks]
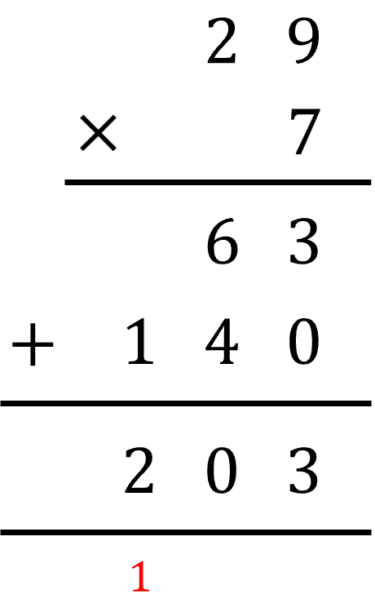
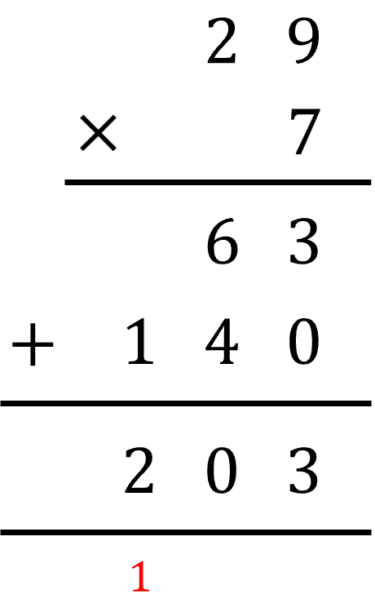
This question is asking us about proportion, how many blocks can be painted per tin of paint?
87 \div 3 = 29 wooden blocks can be painted per tin of paint.
Then, use the proportional statement we have found to work out how many wooden blocks can be painted using 7 tins of paint.
If 1 tin of paint is enough to paint 29 wooden blocks then to find how many blocks 7 tins cover, we calculate:
29 \times 7 = 203
So, 7 tins of paint is enough to paint 203 wooden blocks.
Example 4


Tyrone and his friends went to Angelo’s Eatery for some food and drinks.
In total, they ordered 2 burgers, 2 hotdogs, 1 cola and 2 lemonades.
Tyrone pays for the meal with two £ 20 notes.
How much change does he receive?
[3 marks]
This question involves multiplication, addition and subtraction of decimals as well as conversions of money.
First, the price list needs to be changed so that all items are given in consistent units.
Cola: 95\text{p} \div 100 = £0.95
Lemonade: 90\text{p} \div 100 = £0.90
Next, we need to find out how much the items cost in total.
Two burgers: \textcolor{darkturquoise}{2} \times £8.50 = £17.00
Two hotdogs: \textcolor{darkturquoise}{2} \times £6.20 = £12.40
One cola: \textcolor{darkturquoise}{1} \times £0.95
Two lemonades: \textcolor{darkturquoise}{2} \times £0.90 = £1.80
Then, add these items altogether to find the total price.
£17.00 + £12.40 + £0.95 + £1.80 = £32.15
In the question, it says Tyrone paid with two £20 notes.
\textcolor{darkturquoise}{2} \times £20 = £40
So, to find the change that Tyrone will receive, subtract the total cost from the money he pays with.
£40 - £32.15 = £7.85
Word Problems Example Questions
Question 1: Catherine is thinking of a positive number.
If she squares her number and adds 1, she gets 17.
What was Catherine’s original number?
[2 marks]
For this question, your child needs to work backwards, like they are solving an equation.
The last thing that happened was Catherine \textcolor{red}{+1} so the first thing to do is to \textcolor{red}{-1}.
17 \textcolor{red}{- 1} = 16
Catherine squared her number originally so we need to find a number that when squared is equal to 16.
The only positive number that this is true for is 4. Therefore, Catherine’s number must be 4.
Question 2: Mariam takes an exam that has 120 marks in total.
Mariam receives her results and has answered 108 of the total marks correctly.
What percentage of the marks did Mariam get incorrect?
[3 marks]
To find the number of marks she got incorrect, subtract the marks she got correct from the total marks available.
120 - 108 = 12
Now, we can form a fraction with incorrect marks on the numerator and total marks on the denominator.
\dfrac{12}{120}
We need to find an equivalent fraction that has a denominator of 100.
\dfrac{12 \div 12}{120 \div 12} = \dfrac{1}{10}
\dfrac{1 \times 10}{10 \times 10} = \dfrac{10}{100}
So, the percentage of incorrect marks is 10\%
Question 3: Harper buys 5 packets of crisps that all cost the same price.
She pays with a £10 note and receives £4.25 in change.
How much does one of the packets of crisps cost?
[2 marks]
The 5 packets of crisps altogether cost:
£10 - £4.25 = £5.75
One individual packet of crisps costs a fifth of this price.
£5.75 \div 5 = £1.15

