Area
Area of 2D Shapes
The area of a 2D shape is the size of the surface the shape covers. In the 11+, your child is expected to be able to find the area of 2D shapes including quadrilaterals, triangles and circles.
Working through the content on this page and the examples will help your child become more confident with finding the area of 2D shapes.
Area of a Rectangle
The area of a rectangle or a square is the simplest area for your child to calculate.
Multiply the length by the width of the rectangle or square to get the area
Example: Work out the area of the rectangle below.

To calculate the area of a rectangle, multiply the length by the width so the area is:
12 \times 4.5 = 54
The unit used for area in this example is \text{cm}^{2} so the area of the rectangle is 54\text{ cm}^{2}
Area of a Triangle
To find the area of a triangle, your child needs to know and be able to use the following formula.
Area of a triangle = \dfrac{1}{2} \times base \times height
Example: Find the area of the triangle below.
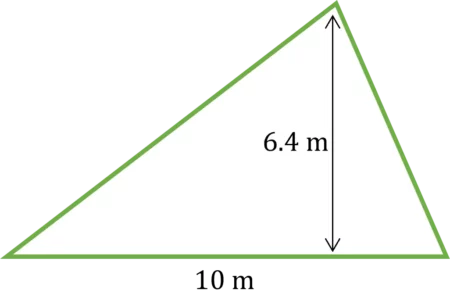
Use the formula for the area of a triangle:
Area = \dfrac{1}{2} \times 10 \times 6.4
So, the area of the triangle is 32\text{ m}^{2}
Area of a Circle
The area of a circle is a bit different to the rectangles and triangles we have looked at before. To find the area of a circle we will need \pi = 3.14.
To find the area of a circle, your child should follow the steps below:
- Find the radius of the circle.
- Multiply the radius by itself (or square it)
- Then multiply the result by \bold{\textcolor{purple}{3.14}}
Example: Find the area of the circle below.
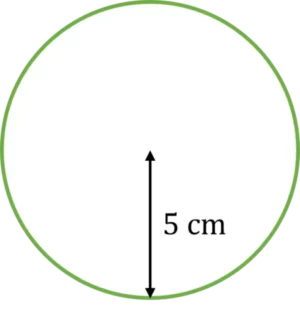
The radius of this circle is 5\text{ cm}.
Next, square the radius.
5^{2} = 5 \times 5 = 25
Then multiply the result by \pi = 3.14
25 \times 3.14 = 78.5
So, the area of the circle is 78.5\text{ cm}^{2}
Example: Compound Shape
Sometimes your child may come across a question that asks for the area of a compound shape. A compound shape is a 2D shape that looks like some of the shapes we’ve seen before but stuck together!
Example: Find the area of the compound shape below.

The first thing your child needs to do when finding an area of a compound shape is to split the area into shapes that they do know how to find the area of.
In this case, the shape can be split into 2 rectangles.
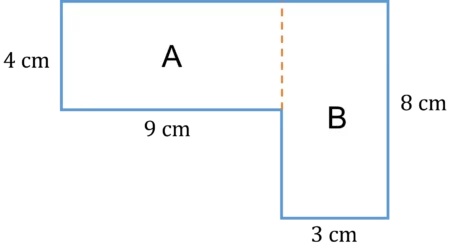
Now that the compound shape is split into easier to deal with shapes we can find the area.
Rectangle A:
Area = 4 \times 9 = 36\text{ cm}^{2}
Rectangle B:
Area = 8 \times 3= 24\text{ cm}^{2}
Then the total area of the compound shape is the areas of the two rectangles added together.
Total area = 36 + 24 = 60\text{ cm}^{2}
Area Example Questions
Question 1: Carol wants to put up 6 identical fence panels next to each other in her garden.
The measurements of 1 of the panels can be seen below.
What is the total area of the 6 fence panels?
[2 marks]
As the fence panels are identical, we need to find the area of 1 of the panels and then multiply that value by 6.
Area of 1 panel =2.5 \times 0.5 = 1.25\text{ m}^{2}
Total area of all 6 panels = 1.25 \times 6 = 7.5\text{ m}^{2}
Question 2: Find the area of a circle with a diameter of 18\text{ cm}.
[3 marks]
Recall that the diameter is the distance from one side of the circle to the opposite side as seen below:
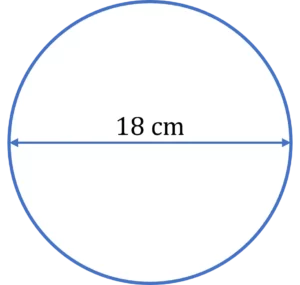
When working out the area of a circle we need the radius.
Radius = 18 \div 2 = 9\text{ cm}
Next, square the radius:
9^{2} = 9 \times 9 = 81
Finally, multiply this value by \pi = 3.14
Area of the circle =81 \times 3.14 = 254.34\text{ cm}^{2}
Question 3: Find the area of the triangle below.
[1 mark]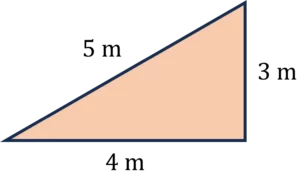
The formula for calculating the area of a triangle is:
Area =\dfrac{1}{2} \times base \times height
In this example we are given all three sides, it is important that we use the correct ones when substituting into the formula.
The base = 4\text{ m}
The height =3\text{ m}
So, the area of the triangle can be worked out:
\dfrac{1}{2} \times 4 \times 3 = 6\text{ m}^{2}

