Factors and Multiples
Factors and Multiples
In their exam, your child may be asked to find prime factors, the lowest common multiple (LCM) and the highest common factor (HCF) of a number or pair of numbers.
In this section, we will show you techniques and examples that you can go through with your child including prime factor trees, so that your child can become familiar with these types of questions.
Prime Factorisation
As the name suggests a prime factor is a factor of a number that also is a prime number.
A prime number is a number whose only factors are \bold{\textcolor{darkturquoise}{1}} and itself. For example 11 is a prime number and the only numbers that divide into it are 1 and 11.
To find the prime factors of a number your child can use a prime factor tree which is a visual way to see how the number is being broken down into its prime factors.
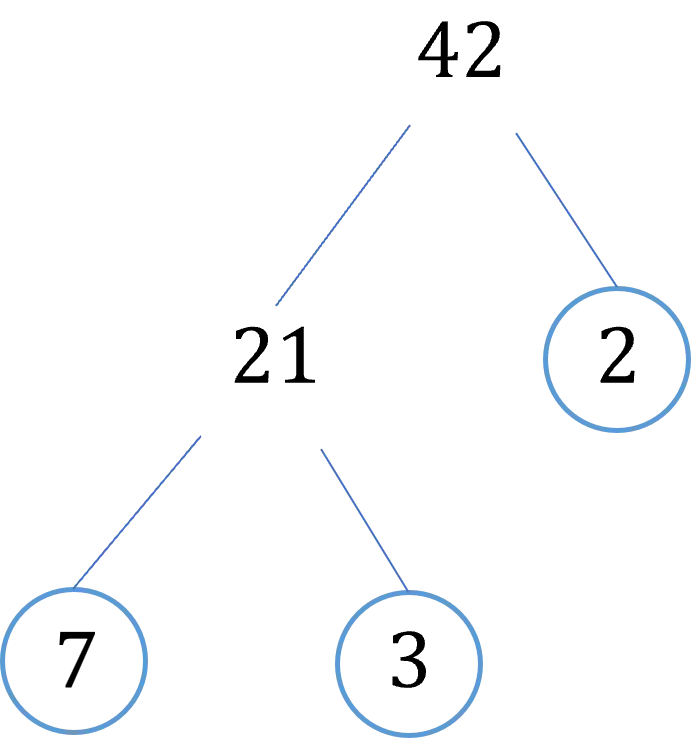

Example: Using a prime factor tree, find the prime factorisation of 42.
First, find two numbers that multiply together to make 42
We have chosen 21 \times \textcolor{red}{2} = 42
Next circle any prime numbers that appear, in this case \textcolor{red}{2} is a prime number so it has been circled. 21 is not prime so we leave that as it is.
Then, do the same for the 21. Two numbers that multiply to make 21 are 7 and 3.
\textcolor{red}{7} \times \textcolor{red}{3} = 21
Both \textcolor{red}{7} and \textcolor{red}{3} are prime so we circle both of them.
The process finishes when at the end of each branch is a prime number that can’t be split up any more. Then, we can write out original number as a product of its prime factors.
42 = \textcolor{red}{2} \times \textcolor{red}{3} \times \textcolor{red}{7}
Lowest Common Multiple (LCM)
The lowest common multiple of two numbers is the smallest value that is a multiple of both numbers.
Example: Find the lowest common multiple of 4 and 6
List out the multiples of both numbers.
Multiples of 4: 4,\,\,8,\,\,\textcolor{orange}{12},\,\,16,\,\,20,\,\,24...
Multiples of 6: 6,\,\,\textcolor{orange}{12},\,\,18,\,\,24,\,\,30,\,\,36...
Therefore, we can see the smallest number that appears in both lists is \textcolor{orange}{12}. It is worth noting that 24 also appears in both lists, but in order for a number to be the lowest common multiple it needs to be the smallest number that appears in both lists.
Highest Common Factor (HCF)
The highest common factor of two numbers is the biggest number that is a factor of both numbers.
Example: Find the highest common factor of 36 and 54
Factors of 36: 1,\,\,2,\,\,3,\,\,4,\,\,6,\,\,9,\,\,12,\,\,\textcolor{purple}{18} and 36
Factors of 54: 1,\,\,2,\,\,3,\,\,6,\,\,9,\,\,\textcolor{purple}{18},\,\,27 and 54
Therefore, we can see that the biggest number that appears in both lists is \textcolor{purple}{18}. Like in the previous example about LCM, there are multiple numbers that appear in both lists but \textcolor{purple}{18} is the greatest which makes it the highest common factor.
Example 1: LCM and HCF Using Prime Factorisation
An alternative method for finding the LCM and HCF of two numbers is to use their prime factorisation.
Example: Find the lowest common multiple and highest common factor of 12 and 8 using prime factorisation.
First, let’s find the prime factorisations of the numbers in the question.
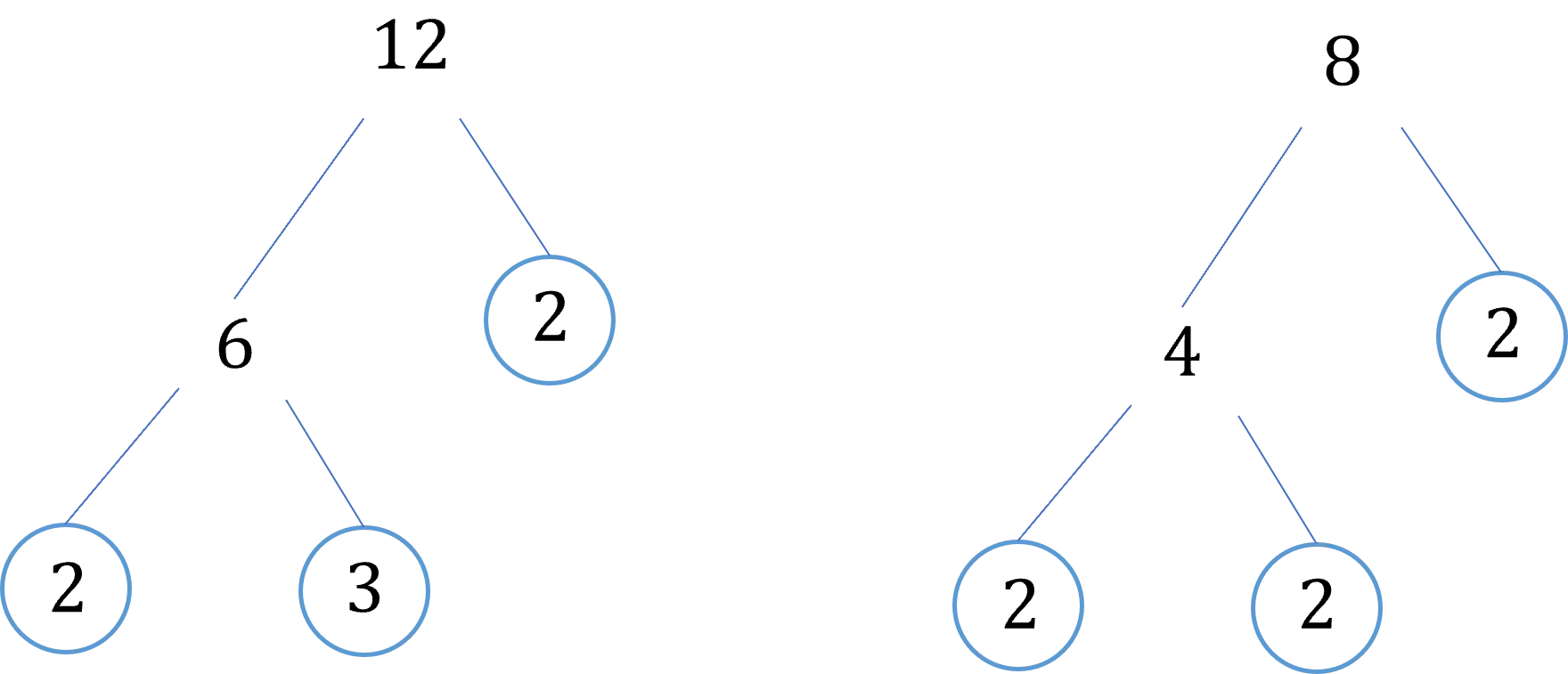
Using the prime factor trees we can write the numbers as a product of their prime factors.
12 = 2 \times 2 \times 3
8 = 2 \times 2 \times 2
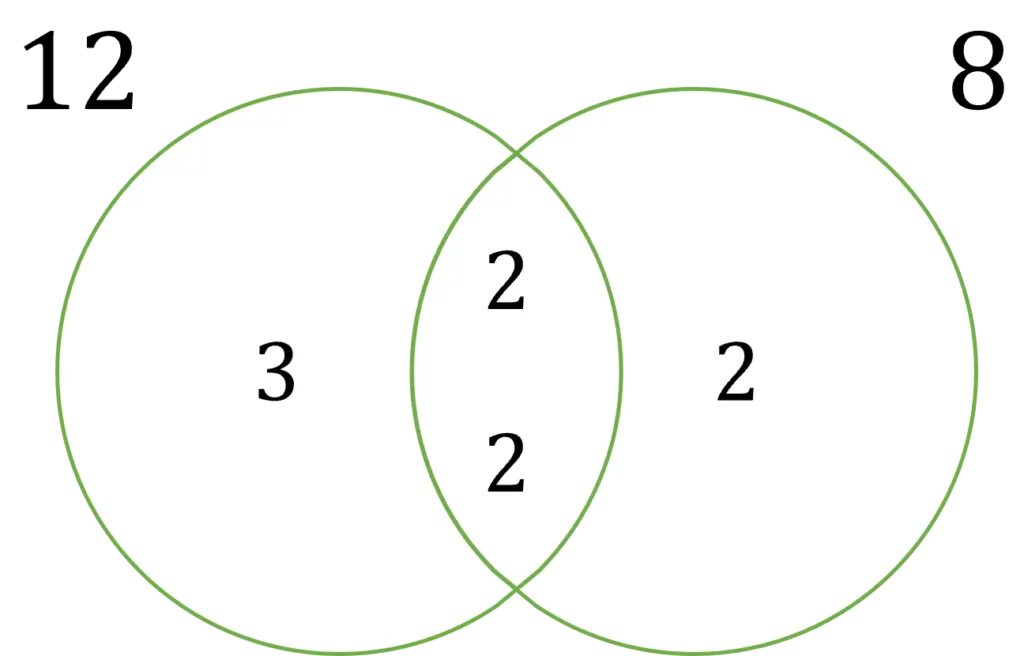

Put the factors into a Venn diagram, the factors that appear in both factorisations go into the middle and the rest in their respective sections.
To find the LCM, multiply all of the numbers found in the Venn diagram.
LCM = 2 \times 2 \times 2 \times 3 = \textcolor{blue}{24}
To find the HCF, multiply the numbers in the middle section of the Venn diagram together.
HCF = 2 \times 2 = \textcolor{red}{4}
Factors and Multiples Example Questions
Question 1: Find the prime factorisation of:
a) 120
b) 72
[2 marks]
a) Draw a prime factor tree for 120 and split up each number until all numbers on the end of the branches are prime numbers. 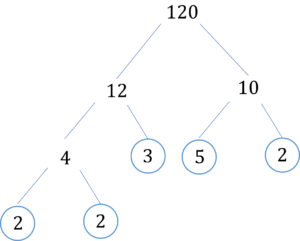
Hence, 120 written as a product of its prime factors is:
120 = 2 \times 2 \times 2 \times 3 \times 5
b) Draw a prime factor tree for 72 and split up each number until all numbers on the end of the branches are prime numbers.
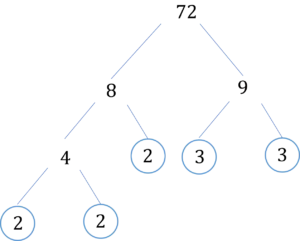
Hence, 72 written as a product of its prime factors is:
72 = 2 \times 2 \times 2 \times 3 \times 3
Question 2: Holly is hosting a party and is serving burgers to the guests.
Burgers can be bought in packs of 6 and bread rolls can be bought in packs of 20.
Holly needs exactly the same amount of burgers as bread rolls.
What is the smallest number of packs of each she must buy?
[3 marks]
The first step is to recognise that to find the answer for this question, we first need to find the lowest common multiple (LCM) of 6 and 20.
Find the prime factor trees of 6 and 20: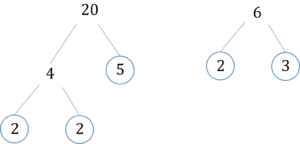
20 = 2 \times 2 \times 5
6 = 2 \times 3
Putting these numbers into a Venn diagram, we can see that the LCM of 6 and 20 is \textcolor{blue}{60} = 2 \times 2 \times 3 \times 5.
Therefore, we need 60 burgers and 60 bread rolls.
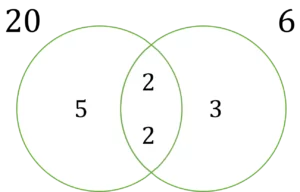
Remember, the question asks us how many packs of each item we will need.
60 \div 6 = 10 packs of burgers
60\div 20 = 3 packs of bread rolls.
Question 3: What is the largest whole number that is a factor of 42 and 54?
[2 marks]
List the factors of 42 and 54.
Factors of 42: 1,\,\,2,\,\,3,\,\,\textcolor{red}{6},\,\,7,\,\,14,\,\,21 and 42
Factors of 54: 1,\,\,2,\,\,3,\,\,\textcolor{red}{6},\,\,9,\,\,18,\,\,27 and 54
The largest number in both of the lists is \textcolor{red}{6}. So, this is the largest whole number that is a factor of both numbers.