Mean
Mean
When we have a set of data, we might want to analyse the data to find out more about it. One way that we can analyse the data is to find the mean or average of the set of data.
In this topic, we will go through some examples which will help your child become comfortable with finding the mean and analysing data in their exam.
Finding the Mean
The mean is a value which summarises the data set as it is the average value.
To find the mean your child needs to follow 2 simple steps.
- Add up all the numbers in the data set.
- Then divide that sum by the number of data points there are.
Example: Find the mean of the data set below.
8,\,\,\,6,\,\,\,9,\,\,\,10,\,\,\,7,\,\,\,8
- Add up all the numbers in the set of data.
8+6+9+10+7+8=48
- Then divide that sum by the number of data points there are.
In this data set there are \bold{\textcolor{darkturquoise}{6}} values so there are \bold{\textcolor{darkturquoise}{6}} data points.
48\div 6 = 8
So, the mean of the data set is 8
Example: Finding the Mean from a Bar Chart
Sometimes your child might not be given a list of numbers and asked to find the mean. They might have to interpret a graph or a bar chart to find the numbers and then have to find the mean.
Example: Solomon owns a shop. He monitors how many books he sold each day across one week in the bar chart below.
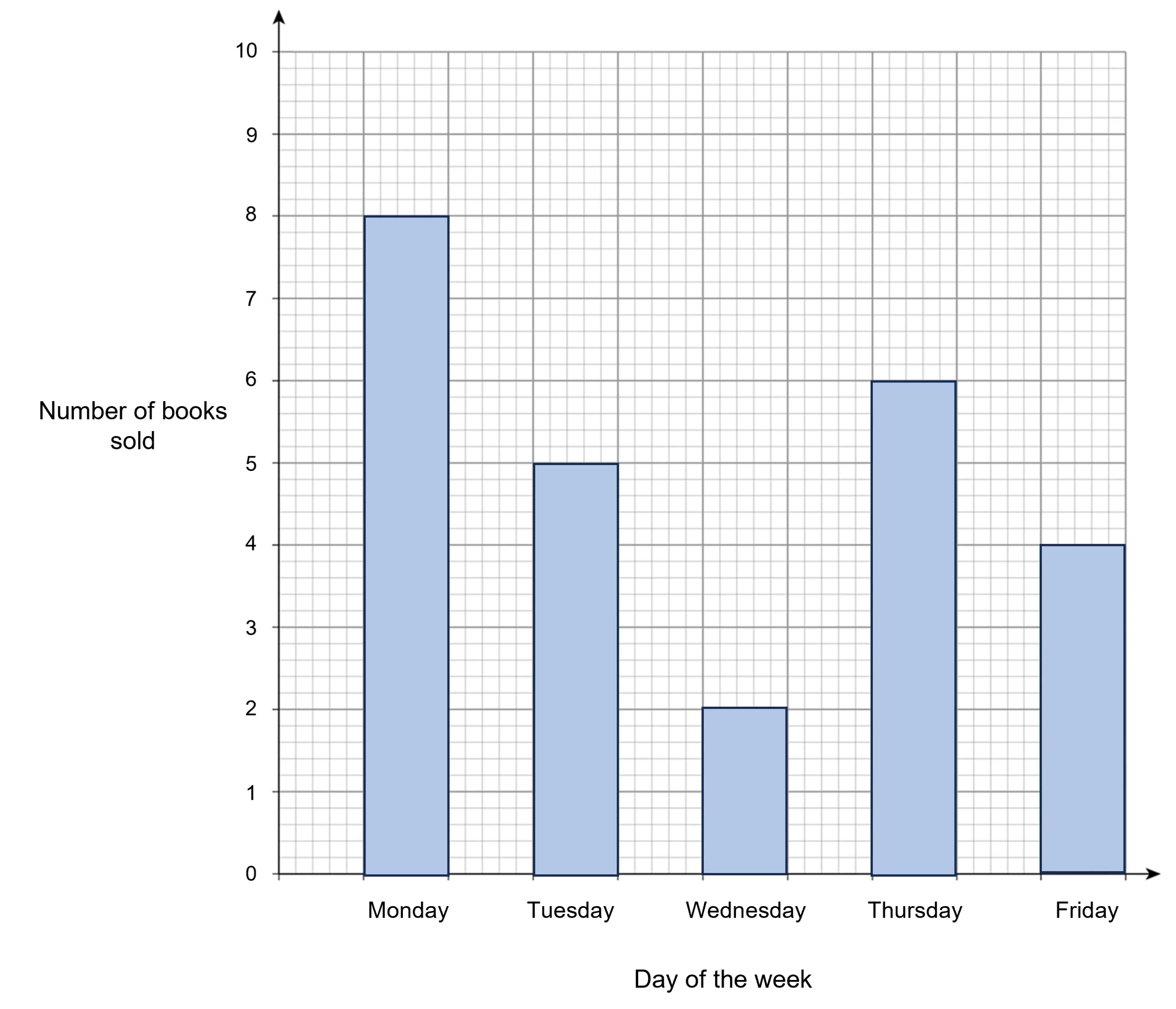
Find the mean number of books that were sold across the week.
First, we need to able to extract the data from the bar chart.
Monday: 8 books were sold.
Tuesday: 5 books were sold.
Wednesday: 2 books were sold.
Thursday: 6 books were sold.
Friday: 4 books were sold.
Now, we have our set of data. If your child finds it easier they can write the set of data in a list.
8,\,\,\,5,\,\,\,2,\,\,\,6,\,\,\,4
Then, find the mean as usual.
- Add up the numbers.
8+5+2+6+4 = 25
- Divide by the number of data points.
In this case there are five data points:
25\div 5 = 5
So, the mean number of books that were sold across the week is 5 books.
Mean Example Questions
Question 1: Find the mean of each of the sets of data.
a) 12,\,\,15,\,\,10,\,\,7
b) 2,\,\,1,\,\,6,\,\,4,\,\,4,\,\,3,\,\,8
[4 marks]
a) Add up the numbers in the list.
12+15+10+7 = 44
Divide by the number of data points, which is 4 in this question.
44\div 4 = 11
So, the mean is 11
b) Add up the numbers in the list.
2+1+6+4+4+3+8 = 28
Divide by the number of data points, which is 7 in this question.
28 \div 7 = 4
So, the mean is 4
Question 2: Stefan records the temperature outside their house in degrees Celsius at five different points of the day.
His results were:

The mean temperature was 16 degrees Celsius.
What temperature did Stefan record at 3pm?
[3 marks]
To find the missing temperature, we need to work backwards from the mean.
So, instead of dividing the sum of values by the number of data points, we need to multiply the mean by the number of data points.
16 \times 5 = 80
We multiply by five because the mean was calculated with all five data points.
Now we know that all five numbers added together make 80.
We know four of these numbers, so to find the missing value at 3pm, we simply subtract the other four values from 80.
80 - 15 - 17 - 16 - 14 = 18
So, the temperature recorded at 3pm was 18 degrees Celsius.
Question 3: Josh collects some information about the price of a cup of tea in 4 different tea shops near his house.
The prices he collects are:
£2.50,\,\,\,£2.10,\,\,\,£1.90,\,\,\,£2.30
What is the mean price of a cup of tea in his local area?
[2 marks]
We can still work out the mean in the same way even with decimal values.
- Add up the numbers.
2.5 + 2.1 + 1.9 + 2.3 = 8.8
- Divide the sum by the number of data points there are.
8.8 \div 4 = 2.2
So, the mean price of a cup of tea in Josh’s local area is £2.20