Multiplication and Division
Multiplication and Division
Multiplication and division are fundamental skills that underpin a lot of questions that your child may get asked on their exam. It is important that they have a good grasp on the techniques used in this section. We will also look at tricks for multiplying and dividing by 10,\,100 and 1000.
Multiplying by \boldsymbol{10,\,100} and \boldsymbol{1000}
These are some helpful rules for your child to learn to make multiplying easier!
- Multiplying by \textcolor{green}{10}: move the decimal point \textcolor{green}{1} place to the right.
- Multiplying by \textcolor{green}{100}: move the decimal point \textcolor{green}{2} places to the right.
- Multiplying by \textcolor{green}{1000}: move the decimal point \textcolor{green}{3} places to the right.
These rules can be generalised for other values such as 10\,000,\, 100\,000 ... just move the decimal point to the right the same number of places as the number has zeros after the 1.
Dividing by \boldsymbol{10,\,100} and \boldsymbol{1000}
Multiplying and dividing are opposite operations, therefore the rules your child needs to remember for division are the opposite of the rules for multiplication.
- Dividing by \textcolor{blue}{10}: move the decimal point \textcolor{blue}{1} place to the left.
- Dividing by \textcolor{blue}{100}: move the decimal point \textcolor{blue}{2} places to the left.
- Dividing by \textcolor{blue}{1000}: move the decimal point \textcolor{blue}{3} places to the left.
Like with the rules for multiplication these rules can be generalised for other values… just move the decimal point to the left the same number of places as the number of zeros after the 1.
Example 1: Multiplication Using a Written Method
Your child can use a method called the written method to multiply large numbers or decimals.
Calculate 43 \times 66
Step \boldsymbol{1}: First, write the numbers one above the other making sure the units, tens and hundreds columns line up. In this case, both numbers are two digits so can be lined up quite easily.
Step \boldsymbol{2}: Next, multiply the digit in the units column of the bottom number by every digit in the top number.
\textcolor{blue}{6} \times 3 = \textcolor{red}{1}8
The \textcolor{red}{1} is carried over as 18 is greater than 10.
\textcolor{blue}{6} \times 4 = 24
Don’t forget to add on the \textcolor{red}{1} that has been carried over!
24 + \textcolor{red}{1} = 25Therefore, \textcolor{blue}{6} \times 43 = 258
Step \boldsymbol{3}: The next row is a little different, we are now multiplying all the digits in the top number by \textcolor{blue}{60} so we must add a \textcolor{purple}{0} to the units column before we begin to multiply.
Now, we can treat it as before and multiply each digit by \textcolor{blue}{6}.
\textcolor{blue}{6} \times 3 = 18
Remember to carry the \textcolor{red}{1}!
\textcolor{blue}{6} \times 4 = 24
24+\textcolor{red}{1} = 25
Therefore, 60 \times 43 = 2580
Step \boldsymbol{4}: Add these values using the column method for addition discussed in an earlier topic.
2580 + 258 = 2838
So,
43 \times 66 = 2838
This method can also be used to multiply numbers with decimal points. A good thing for your child to remember is to always make sure the decimal points of the numbers they are multiplying together are lined up correctly.
Example 2: Bus Stop Method for Division
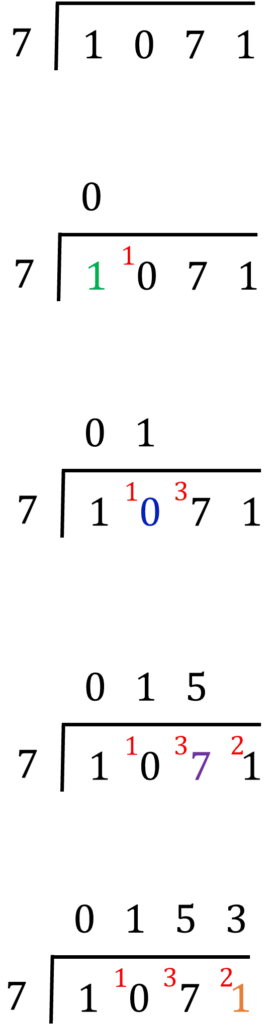
The bus stop method is a memorable way for your child to divide numbers and gets its name as it looks a bit like the number is waiting inside a bus stop.
Calculate 1071 \div 7
Step \boldsymbol{1}: Set up the bus stop. The number we are dividing by, in this case 7, goes outside the bus stop and the number we are dividing into, in this case 1071 goes inside the bus stop.
Step \boldsymbol{2}: Next, see how many times 7 divides into \textcolor{green}{1}. \textcolor{green}{1} is less than 7 so divides 0 times. A 0 goes above the \textcolor{green}{1} on the bus stop and the \textcolor{red}{1} gets carried to the next digit.
This means our next number to divide into is not \textcolor{blue}{0} but is \textcolor{red}{1}\textcolor{blue}{0}.
Step \boldsymbol{2}: Next, how many times does 7 divide into \textcolor{red}{1}\textcolor{blue}{0}? Well 1 \times 7 = 7 so the answer is once with \textcolor{red}{3} leftover.
Step \boldsymbol{3}: Then, how many times does 7 divide into \textcolor{red}{3}\textcolor{purple}{7}? Well 5\times 7 = 35 so the answer is 5 times with \textcolor{red}{2} leftover.
Step \boldsymbol{4}: Finally, how many times does 7 divide into \textcolor{red}{2}\textcolor{orange}{1}? Well 3 \times 7 = 21 so 3 times exactly.
Therefore,
1071 \div 7 = 153
Multiplication and Division Example Questions
Question 1: Calculate the following:
a) 2.4 \times 100
b) 908 \div 100\,000
c) 0.004 \times 10
[3 marks]
a) Multiplying by 100 means we move the decimal point 2 places to the right.
So,
2.4 \times 100 = 240
b) Dividing by 100\,000 means we move the decimal point 5 places to the left as there are 5 zeros after the 1.
So,
908 \div 100\,000 = 0.00908
c) Multiplying by 10 means we move the decimal point 1 place to the right.
So,
0.004 \times 10 = 0.04
Question 2: Michael buys 8 packs of chocolate bars.
Each pack contains 4 individual bars and each individual bar costs £1.20
How much money does Michael spend on chocolate bars altogether?
[2 marks]
Total number of individual chocolate bars bought:
8 \times 4 = 32 bars
Then find the total cost of 32 individual chocolate bars.
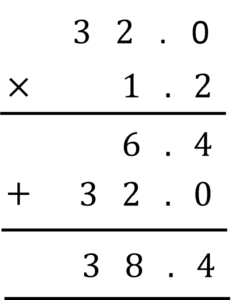Total cost:
32 \times \pounds 1.20 = \pounds 38.40
Question 3: Catherine has 131 cupcakes that she needs to to in boxes to be sent to a bakery.
Each box can fit 8 cupcakes.
How many boxes will she need to transport all of the cupcakes to the bakery?
The calculation needed is:
131 \div 8
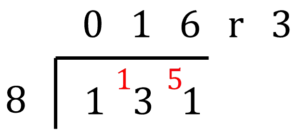
Therefore 8 divides 16 times into 131 with a remainder of 3. This means that the numbers don’t divide exactly.
16 boxes will hold 16 \times 8 = 128 cupcakes but there will be still be 3 cupcakes without a box.
Therefore, 17 boxes are needed to transport all of the cupcakes to the bakery.