Perimeter
Perimeter
The perimeter of a shape is the length around the outside of the shape. Your child needs to be able to work out the perimeter of different shapes including triangles, quadrilaterals and circles.
Working Out the Perimeter
To calculate the perimeter of a 2D shape, your child must add up the lengths of all of the sides.
Key tips:
- Make sure you don’t miss any of the lengths when adding.
- Make sure all of the lengths being added are in the same units.
Some shapes will be harder to calculate as not all of the side lengths will be known. It is important that your child works out any missing side lengths before calculating the perimeter.
Example 1: Simple Shapes
Example: Work out the perimeter of the triangle below.

In this example, all of the side lengths are labelled but they aren’t all using the same units.
First, your child must convert 42\text{ mm} into centimetres.
42 \text{ mm} \textcolor{darkturquoise}{\div 10} = 4.2\text{ cm}
Now, all of the side lengths are in consistent units, we can add them together to find the perimeter.
Perimeter =4.3 + 4.2 + 5.2 = 13.7\text{ cm}
Example 2: Compound Shape
Remember some examples won’t have all of the side lengths labelled and your child will have to work them out before finding the perimeter of the shape.
Example: Find the perimeter of this compound shape.

This shape is missing two of its side lengths so before your child calculates the perimeter remind them to work out the missing lengths first.
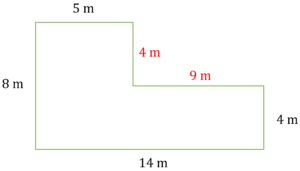

8\text{ m} - 4\text{ m} = \textcolor{red}{4\text{ m}}
14\text{ m} - 5\text{ m} = \textcolor{red}{9\text{ m}}
Therefore, we now have all of the side lengths of the shape and can calculate the perimeter. All of the lengths are in the same units so we can simply add them all together.
5 + 4 + 9 + 4 + 14 + 8 = 44\text{ m}
So, the perimeter of our shape is 44\text{ m}.
Circles – Circumference
The perimeter of a circle is called the circle’s circumference. Your child may have to calculate the circumference of a circle in their exam but it isn’t as simple as finding the perimeter of other shapes.
The circumference is found using the following steps.
- Find the diameter of the circle. Remember the diameter is double the radius!
- Multiply the diameter by a number, \textcolor{purple}{3.14} called \pi (pronounced “pie”)
Example: Find the circumference of a circle with a diameter of 5\text{ cm}.
Using the steps:
- The diameter is 5\text{ cm}
- Circumference =5 \textcolor{purple}{\times 3.14}
So, the circumference is 15.7\text{ cm}.
Perimeter Example Questions
Question 1: Find the perimeter of the regular pentagon below.
[2 marks]
As the shape is a regular pentagon, all of the sides are the same length so we can fill in the missing side lengths.

Now to find the perimeter, simply add up all five sides.
6.25+ 6.25+ 6.25 + 6.25 + 6.25 = 31.25 \text{ mm}
Question 2: The perimeter of the rhombus below is 82\text{ cm}.
Find the value of the side length labelled x.
[1 mark]

Your child needs to be able to recall properties of 2D shapes for this question.
A rhombus has 4 equal sides.
So, the perimeter is equal to x+x+x+x
To find the value of x divide the perimeter of the rhombus by \textcolor{purple}{4}.
x = 82 \textcolor{purple}{\div 4} = 20.5\text{ cm}
Question 3: Find the circumference of the circle below.
The radius of the circle is 4\text{ cm}
[2 marks]
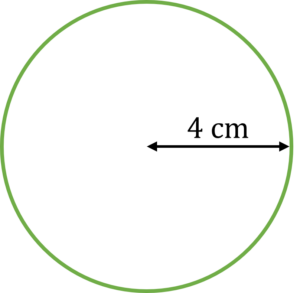
We are told the circle in the question has a radius of \bold{\textcolor{blue}{4\text{ cm}}}
To calculate the circumference, your child should be able to recall that we need the diameter of the circle.
Diameter =\bold{\textcolor{blue}{4}} \times 2 = \bold{\textcolor{red}{8\text{ cm}}}
Now, we can find the circumference.
\bold{\textcolor{red}{8}} \times 3.14 = 25.12\text{ cm}
So, the circumference of this circle is 25.12\text{ cm}.