Probability
Probability
The probability of an event happening is how likely the event is to happen. Probability ranges from impossible to certain and can be given a numerical value.
In this topic, your child should become familiar with this concept and be able to use a probability number line to show an understanding of how likely an event is to happen given context.
Probability Scale
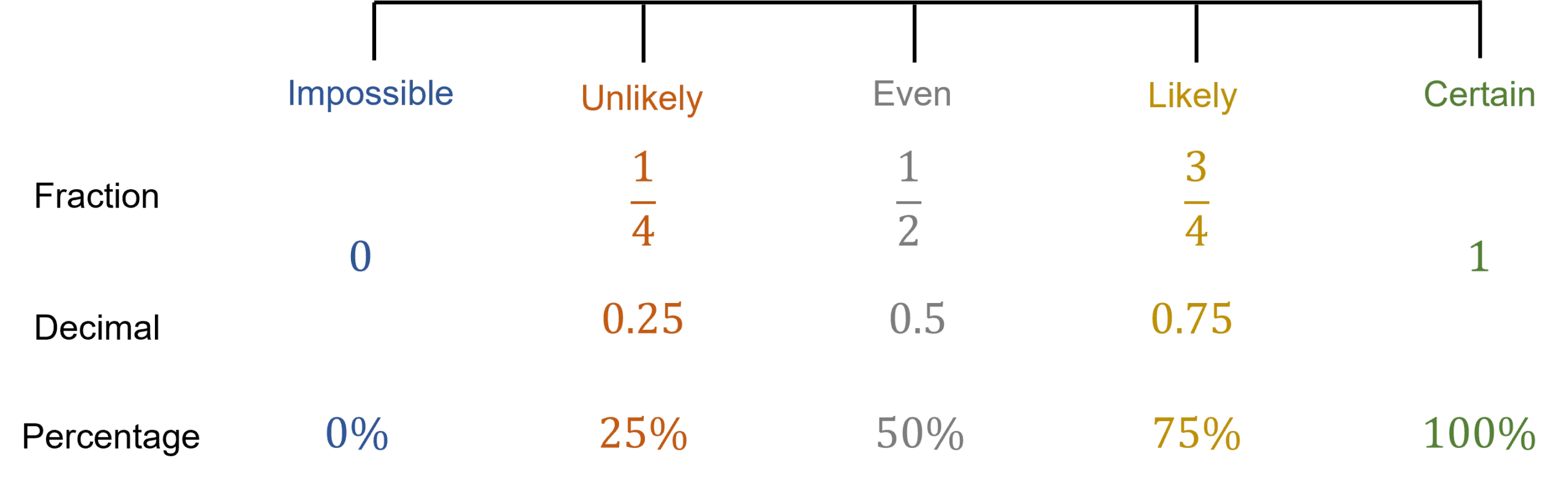
The range of probability is from impossible to certain and can be visualised on the probability scale below.

Your child may be asked to place the probability of an event on the number line.
Alternatively, they may be asked for the probability of an event as a fraction, decimal or percentage.
For a refresher on converting between fractions, decimals and percentages check out the revision page.
The labels ‘likely’ and ‘unlikely’ are used to describe any probability between impossible and even or between even and certain. This means they aren’t always represented by \dfrac{1}{4} and \dfrac{3}{4}.
For example a probability of \dfrac{1}{6} can be described as unlikely as it is between 0 and \dfrac{1}{2}.
- Probabilities should add up to \bold{1} so to find the probability that an event doesn’t happen simply subtract the probability that it does happen from 1.
- All probability is found within this scale, a probability cannot be greater than 1 or less than 0.
Example 1: Number Line
Your child may be asked in their exam to mark the probability of an event onto a number line.
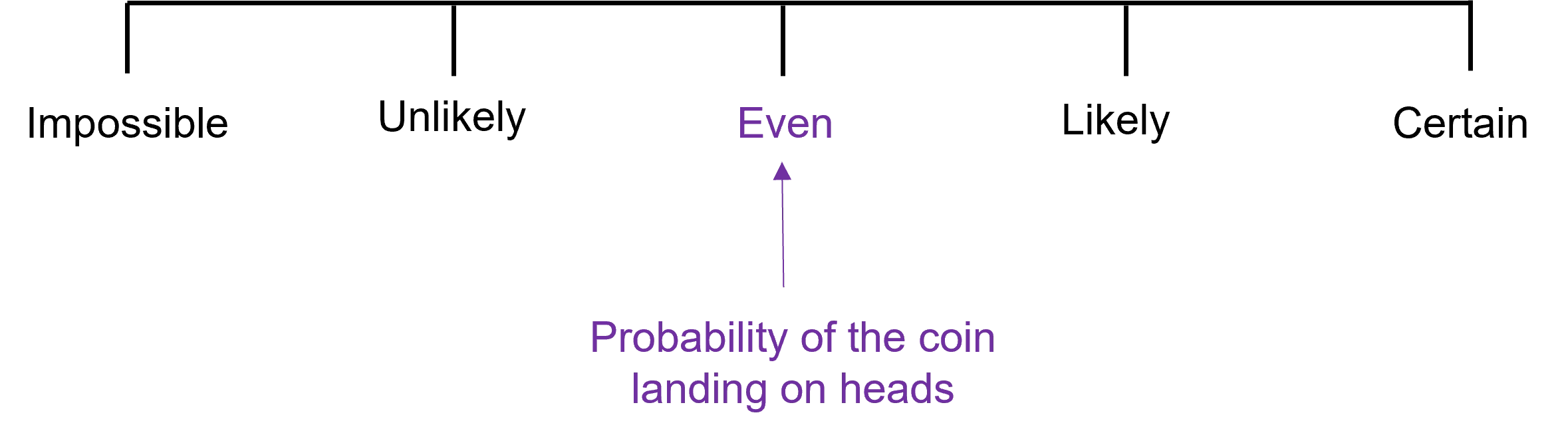
Example: Alan flips a fair coin.
What is the probability that the coin lands on heads?
Mark this probability on a probability scale.
First, we need to consider how many outcomes there are when flipping a coin. There are \bold{\textcolor{darkturquoise}{2}} outcomes: heads and tails.
Out of those outcomes how many are heads? \bold{\textcolor{darkturquoise}{1}}
So, the probability of the coin landing on heads is 1 out of a possible 2 outcomes.
Or we could say a probability of \dfrac{1}{2}
On the scale of probability this will be in the middle as it is an even chance.
Calculating Probabilities
Like we saw in the previous example to calculate the probability of an event, your child needs to find the number of possible outcomes and then find the number of those outcomes that are ways the event can happen.
The probability is then:
\text{Probability } = \dfrac{\textcolor{green}{\text{Number of ways the event happens}}}{\textcolor{blue}{\text{Total number of outcomes}}}
From there, your child can use their skills of converting fractions, decimals and percentages to present their answer how the question wants.
For example, we have a 6 sided fair dice and we want to calculate the probability that when the dice is rolled it will land on a number less than or equal to 2.
So, find the total number of outcomes: 6
Then the number of desired outcomes: 2
These are the number 1 and the number 2
So, the probability is \dfrac{2}{6} = \dfrac{1}{3}
Example 2: Calculating Probabilities
Example: Issa has a bag of marbles.
Inside the bag of marbles is:
3 blue marbles
5 purple marbles
6 pink marbles
6 green marbles
Issa picks one of the marbles out at random.
What is the probability, as a percentage, that the marble is blue?
First, your child needs to find the probability that the marble is blue as a fraction then convert it to a percentage.
Total number of outcomes (total marbles in the bag):
3 + 5 + 6 + 6 = 20 outcomes
Number of blue marbles: 3 blue marbles
So, the probability as a fraction is \dfrac{3}{20}
The question wants our answer as a percentage so we need to convert the fraction to a percentage.
\dfrac{3\times 5}{20 \times 5} = \dfrac{15}{100}
So, the percentage is 15\%
Probability Example Questions
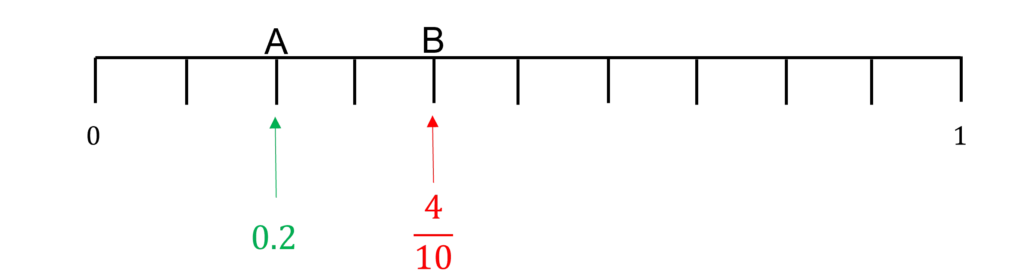
Question 1: The probability that it will rain on Wednesday is 0.8 and the probability that it will rain on Thursday is \dfrac{3}{5}.
Mark the following events on the probability scale below:
A: The probability that it doesn’t rain on Wednesday.
B: The probability that it doesn’t rain on Thursday.
[2 marks]

On Wednesday, the probability that it rains is 0.8 so the probability it doesn’t rain is:
1 - 0.8 = 0.2
On Thursday, the probability that it rained was \dfrac{3}{5} so the probability it doesn’t rain is \dfrac{2}{5}.
\dfrac{2}{5} = \dfrac{4}{10}
These probabilities are shown on the probability scale below:
Question 2: Gwen has a box with 4 red counters, 9 yellow counters, 6 purple counters and 5 brown counters in.
Gwen picks one out of the box at random.
What is the probability that the counter is purple?
Give your answer as:
a) a fraction
b) a decimal
c) a percentage
[3 marks]
a) First, find the number of total outcomes which in this case is the total number of counters in the box.
4 + 9 + 6 + 5 = 24 total outcomes
Now, identify how many purple counters there are: 6 counters.
Then we can form the fraction by putting the number of purple counters as the numerator and the total number of counters as the denominator.
The probability of picking a purple counter is \dfrac{6}{24}
This can be simplified to \dfrac{1}{4}
b) To find this probability as a decimal divide the top number by the bottom number.
1 \div 4 = 0.25
c) Finally, to find the probability as a percentage, multiply the decimal value found in part b) by 100
0.25 \times 100 = 25\%
Question 3: Salma has a fair six-sided dice.
She rolls the dice 120 times.
How many times would Salma expect the dice to land on 3?
[2 marks]
In the question we are told that the dice is fair. This means that there is an equal chance or an equal probability of it landing on each of the numbers.
Your child should be able to identify that the probability of the dice landing on any of the numbers is \dfrac{1}{6} as there are six sides of the dice.
To find how many times Salma would expect a 3 multiply this probability by the number of times the dice is thrown.
120 \times \dfrac{1}{6} = 20 times