Time
Time
Your child will need to know how to read time displayed in different formats, and will need to be familiar with using different units of time. They may also need to work out a time from a worded context.
The \bf{12}-Hour Clock
The hours on a \bf{12}-hour clock are shown by the numbers 1-12. We need to add \textbf{am} or \textbf{pm} to show whether the time is in the morning or the afternoon.
Times with \textbf{am} are between midnight and 11:59 in the morning.
Times with \textbf{pm} are between noon and 11:59 at night.

The \bf{24}-Hour Clock
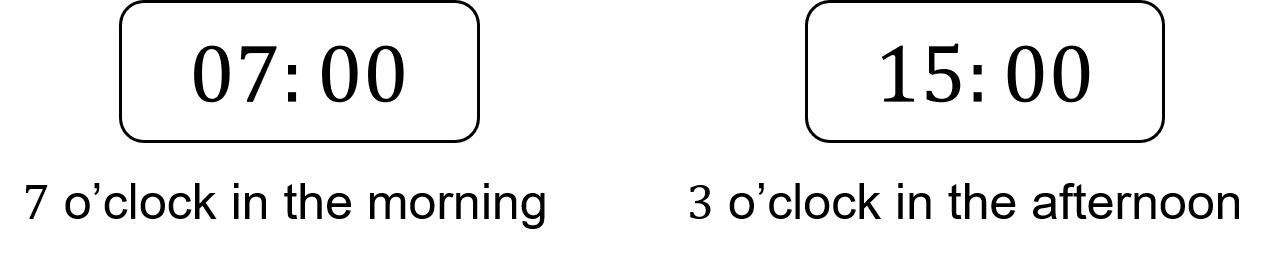
\bf{24}-hour times are the same as 12-hour times in the morning, e.g. 7:00\text{ am} is the same as 07:00 on a 24-hour clock.
If it’s afternoon or evening, for the 24-hour clock we need to add \bf{12} onto the time, e.g. 3:00\text{ pm} is 15:00 on a 24-hour clock.
At midnight, the 24-hour clock goes from 23:59 to 00:00
24-hour times always have \bf{4} digits.
Units of Time
Here’s how some different units of time are related to each other:
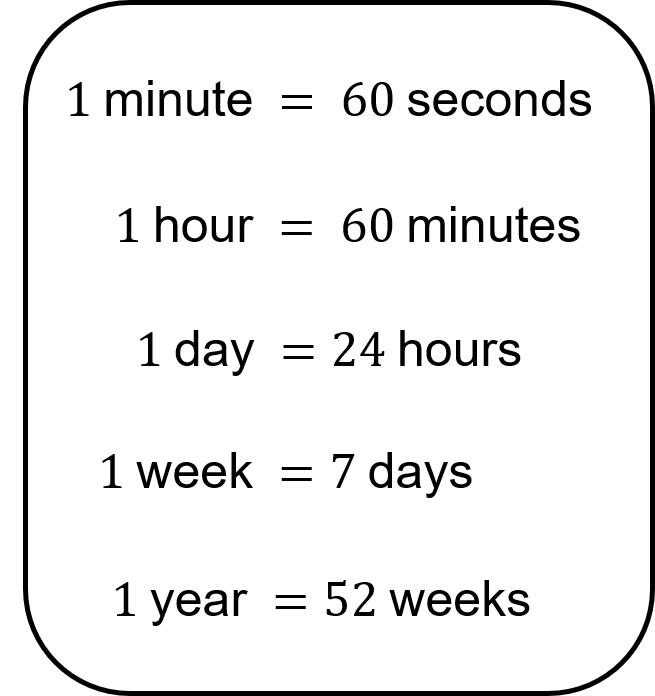

- 1 year has 365 days, or 366 in a leap year. A leap year happens every four years, when an extra day is added to February.
- There are 12 months in a year, but the number of days in each month is different. Your child might find the rhyme below helpful:

Example \bf{1}: Using a \bf{24}-Hour Clock
Your child may need to convert between 12-hour and 24-hour times.
Example: Which of these 24-hour times is the same as quarter to four in the afternoon?

Quarter to four in the afternoon is \bf{3:45}\textbf{ pm} in 12-hour format.
Because the time is in the afternoon, we need to add \bf{12} hours to convert to the 24-hour format.
3:45+12 hours =15:45, so the answer is B.
Example \bf{2}: Converting Between Units of Time
Your child may also need to convert between different common units of time.
Example: Toby puts a tub of pasta in the microwave for 3 and a half minutes. How many seconds is this?
Remind your child that \bf{1} minute is the same as \bf{60} seconds
So \bf{3} minutes must be \bf{3\times60=180} seconds
Half a minute must be \bf{60\div2=30} seconds
So \bf{3} and a half minutes is \bf{180+30=210} seconds.
Example \bf{3}: Calculating a Time
Sometimes your child may need to calculate a time from some given information.
Example: Harry needs to be at the dentist in town by 3:15\text{ pm}. It takes him 2 minutes to walk from his house to the garage where he stores his car. It then takes him 12 minutes to drive to the carpark in town. Finally, it takes him 8 minutes to walk from the carpark to the dentist. What is the latest he can leave his house?
It is helpful to break the journey down into sections using the information given:
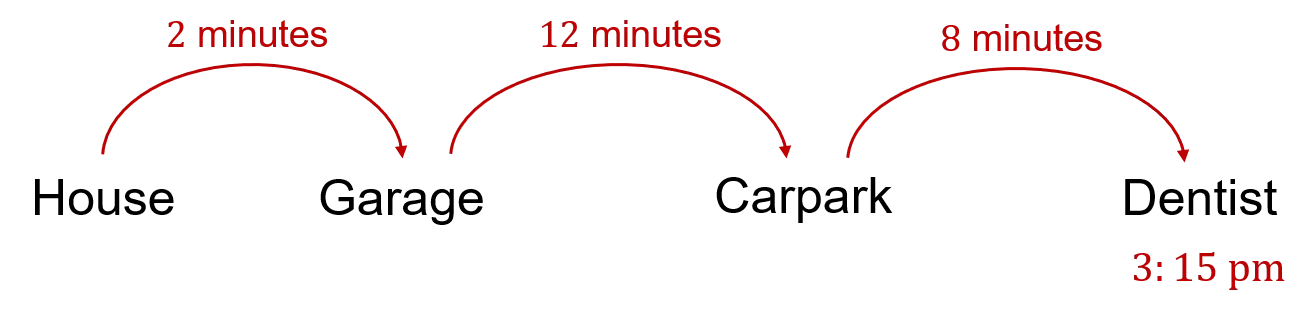
We know Harry needs to be at the dentist by 3:15\text{ pm}, so we need to count back through each stage of the journey.
If we start at 3:15\text{ pm} and count back 8 minutes, we get to 3:07\text{ pm}.
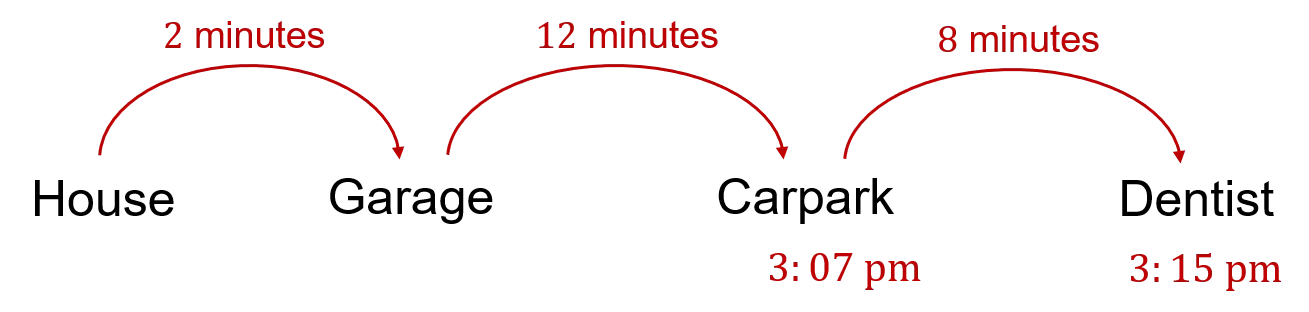
We then need to count back another 12 minutes to find what time he needs to leave his garage. Counting back 7 minutes takes us to 3:00\text{ pm}, and then counting back the remaining 5 minutes takes us back to 2:55\text{ pm}.
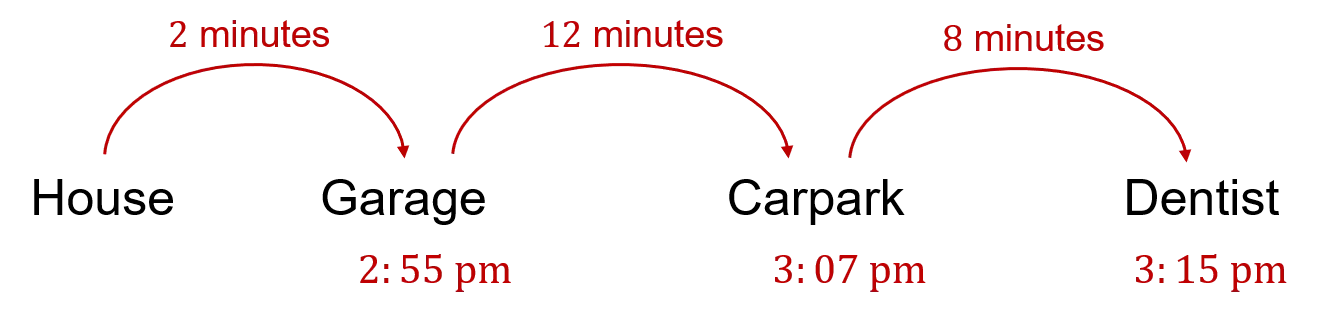
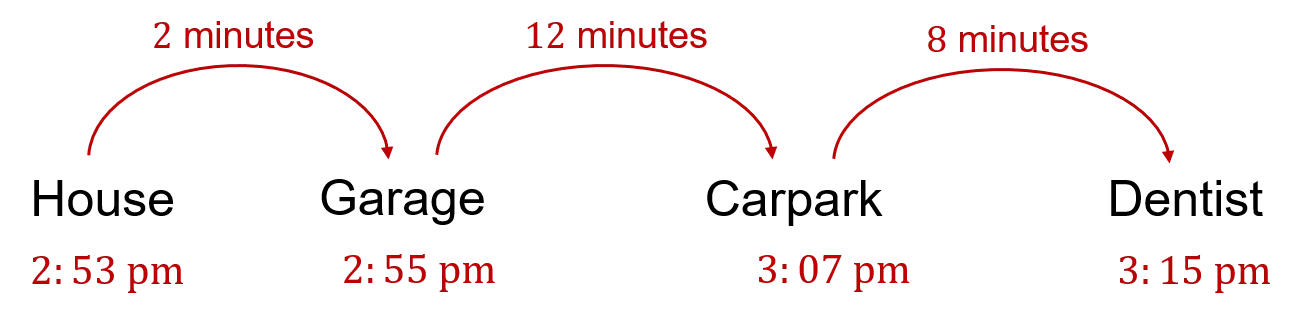
Finally, we need to count back a further 2 minutes to find when Harry needs to leave his house.
Counting back 2 minutes from 2:55\text{ pm} takes us to 2:53\text{ pm}.
So the latest Harry can leave his house is 2:53\text{ pm}.
Time Example Questions
Question 1: The time in Paris is 8 hours behind Sydney, Australia.
In Sydney it is 06:00. What time is it in Paris? Give your answer using the 24-hour clock.
[1 mark]
In Sydney it is 6 o’clock in the morning. Counting back 8 hours, in Paris it must be 10 o’clock at night.
Using the 24-hour clock, we need to add 12 onto 10, so in Paris it is 22:00
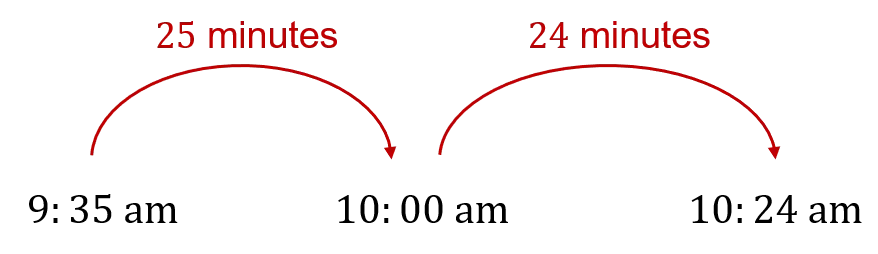
Question 2: John went to visit a friend. He set off at 9:35\text{ am} and arrived at 10:24\text{ am}.
How many minutes did the journey take?
[1 mark]
It would take 25 minutes to 10:00\text{ am}, and then another 24 minutes to 10:24\text{ am}.
25+24=49 minutes in total
Question 3: Peter completed a race in 2 hours and 10 minutes.
a) How long is this in minutes?
b) How long is this in seconds?
[2 marks]
a) 1 hour is 60 minutes.
So 2 hours is 2\times60=120 minutes
120+10=130 minutes in total.
b) 1 minute is 60 seconds.
So 130 minutes is 130\times60=7800 seconds.

